
はじめに
こんにちは、AI・アナリティクス本部、マーケティングサイエンスブロックの青山です。普段は、TVCM等の新規顧客向けの獲得施策や、既存顧客向けの施策など、マーケティング施策の効果検証を担当しています。施策の効果検証においては、平均的な施策効果だけでなく、ユーザーごとの施策効果の違いを捉えることが重要です。そうしたユーザーごとの施策効果を推定する手法は数多くある一方で、実データへの有効性が分からず利用されるケースは少ないという課題がありました。今回の記事では、この課題に対してユーザーごとの効果を求める手法の実用性を検証した取り組みをご紹介します。
目次
背景
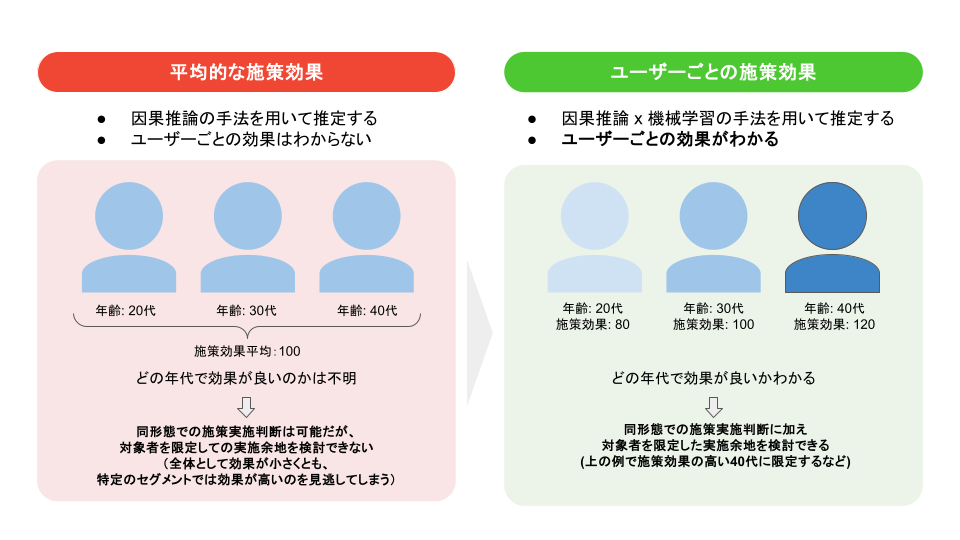
AI・アナリティクス本部、マーケティングサイエンスブロックでは、ZOZOTOWNで実施されている施策の効果検証を日々行なっています。施策効果は主にA/Bテストを実施することで推定していますが、施策効果を最大化するためにはA群、B群の2群の差だけではなく、ユーザーごとの施策効果を知る必要があります。ユーザーごとの施策効果は、因果推論の手法を用いて推定できます。ユーザーごとの施策効果を知ることで、施策を継続して実施する際に活用できる情報が得られます。
例えば、「どのような属性のユーザーに施策を当てるべきか」といった、対象者の最適化を行うことが可能になります。
課題
ユーザーごとの施策効果を推定するための分析手法は数多くある一方で、下記の項目が明らかになっていませんでした。
- 適切な手法:どの手法を利用するのが良いか
- 推定精度:どの程度の精度で推定できるのか
適切な手法:どの手法を利用するのが良いか
分析設計
ここでは、複数の手法を横並びで比較しました。使用したデータは、ZOZOの実際の受注データです。実データに対して、年齢ごとに異なる施策効果と、直近30日の訪問回数を交絡因子として想定した効果を加え半人工的なデータセットを作成しました。変数ごとの関係のイメージは下図になります。
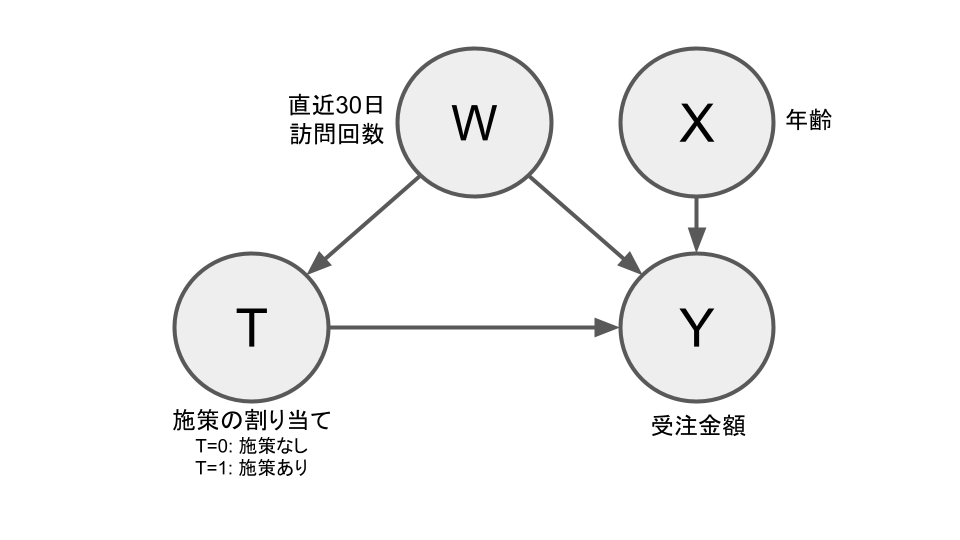
検証の概要をまとめたものが下記の表になります。今回のケースでは年齢ごとに効果が異なるとしているため、効果修飾子は年齢になります。精度指標としては、誤差(MSE)/平均の施策効果(ATE)を用いて評価しました。
数式で整理すると、まずユーザー$i$の施策効果$\tau_{i}$は、施策あり$T=1$と施策なし$T=0$の結果$Y_{i}$の差分になります。
$$ \tau_i = Y_i(T=1) - Y_i(T=0) $$
誤差(MSE)と平均の施策効果(ATE)はそれぞれ下記のように定義されます。式中の$\hat{\tau}_i$は施策効果の推定値になります。そのため誤差(MSE)は各サンプルごとの真の施策効果からのずれを以って評価していることになります。また、平均の施策効果は各サンプルの施策効果を平均した値になります。
$$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (\tau_i - \hat{\tau}_i)^2 $$
$$ \text{ATE} = \frac{1}{n} \sum_{i=1}^n \tau_i $$
| 項目 | 設定 |
|---|---|
| 比較した手法 | Meta-Learner(S, T, X, DR) / Linear DML / Causal Forest DML |
| 使用データ | 半人工データ(実データをベースにシミュレーションした施策効果を合成したデータ) |
| サンプル数 | 10,000 |
| アウトカム($Y$) | 購入金額 |
| 効果修飾子($X$) | 年齢 |
| 交絡因子($W$) | 直近30日の訪問回数 |
| 仮定した施策効果の構造 | ユーザーの年齢に対して線形 / 非線形 |
| 仮定した施策効果の大きさ | 施策がなかった場合の20% |
| 精度の評価指標 | MSE / ATE |
| シミュレーション回数 | 3回 |
結果
結果としては下記の表になりました。精度は、簡単のためS-Learner対比で記載しています。結果DML系の手法で最も精度が良い結果になりました。
| 手法 | MSE / ATE(線形) | MSE / ATE(非線形) |
|---|---|---|
| S-Learner | 100.0% | 100.0% |
| T-Learner | 467.5% | 442.8% |
| X-Learner | 239.5% | 263.8% |
| DR-Learner | 34.0% | 33.0% |
| Linear DML | 7.3% | 7.5% |
| Causal Forest DML | 12.7% | 11.6% |
前提として各手法の性質は下表のとおりで、DML系の手法がよりロバストな推定を行える点を踏まえると上記の結果は自然だと解釈できます。
| 手法 | 信頼区間の算出 | Wの考慮 | 不均衡データへの対応 | 連続的なTへの対応 | Xについて非線形な効果 |
|---|---|---|---|---|---|
| S-Learner | × | × | × | × | ○ |
| T-Learner | × | × | × | × | ○ |
| X-Learner | × | × | × | × | ○ |
| DR-Learner | ○ | ○ | ○ | × | × |
| Linear DML | ○ | ○ | ○ | ○ | × |
| Causal Forest DML | ○ | ○ | ○ | ○ | ○ |
推定精度:どの程度の精度で推定できるのか
分析設計
1の検証で、精度が最も高い手法であった「Linear DML / Causal Forest DML」に注目しました。その2手法について、実際のケースに近いサンプル数、施策効果を仮定した場合にどの程度の精度が得られるかを検証しました。精度の評価指標としては、誤差(RMSE)/平均の施策効果(ATE)を用いて評価しました。定義としては下記のとおりです。
$$\text{RMSE} = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (\tau_i - \hat{\tau}_i)^2 }$$
これは、平均的な施策効果に対して、どれだけ相対的に誤差が大きいかを示す指標です。検証の概要をまとめたものが下記の表になります。
| 項目 | 設定 |
|---|---|
| 比較した手法 | Linear DML / Causal Forest DML |
| 使用データ | 半人工データ(実データをベースにシミュレーションした施策効果を合成した) |
| サンプル数 | 1,000 / 10,000 / 50,000 |
| 効果修飾子($X$) | 年齢 |
| 交絡因子($W$) | 直近30日の訪問回数 |
| 仮定した施策効果の構造 | 効果修飾子(施策効果の違いの原因になる因子)に対して線形 / 非線形 |
| 仮定した施策効果の大きさ | 施策がなかった場合に対して(5%, 25%, 50%) |
| 評価指標 | RMSE / ATE |
| シミュレーション回数 | 3回 |
仮定した施策効果としては下図のように、線形な場合と非線形な場合の2パターンを考えました。
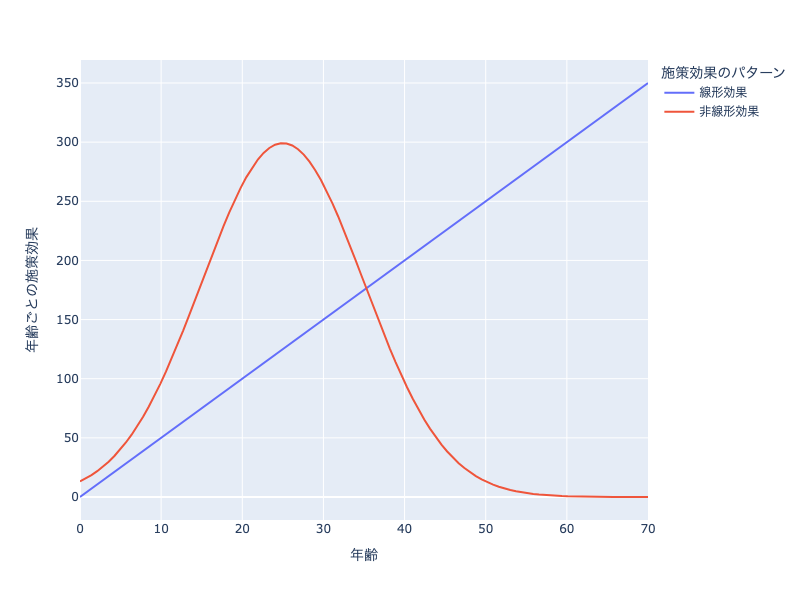
結果
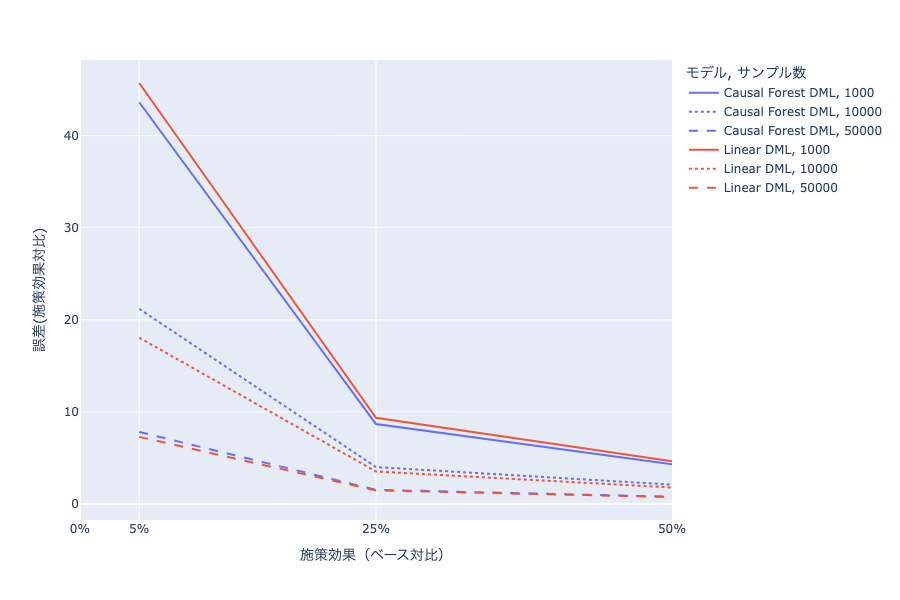
施策効果を変えた場合に誤差(RMSE)/施策効果(ATE)比がどうなるかを下図に示しました。下図を見ると、サンプル数や施策効果が大きくなるほど、誤差(施策効果比)が小さくなっています。数値としては、サンプル数を50,000、ATEを施策がない場合の50%程度にした場合でも誤差/施策効果比は0.7程度になっています。このことから上記の条件下では、施策効果の大小関係については捉えられたとしても、精緻な施策効果の評価は難しいことがわかりました。Linear DMLとCausal Forest DMLの2手法で大きな差はありませんでしたが、施策効果が線形と言えるケースは限られています。そのため、非線形な効果を考慮できるCausal Forest DMLが上記手法の中では最も汎用的で、実務での利用に適していると考えられます。
その他の示唆
検証を進める中で、本題とは少し異なるものの、興味深い気づきも得られました。
1点目として、効果修飾子Xごとの推定精度についてです。
前提としてtree系の手法は、特徴量の両端にあたる領域の推定は不安定になる傾向があります。今回の検証でも、若年層や高年齢層で極端な施策効果を推定しているケースが見られました。これはtree系モデルの構造上、特徴量の端にデータが少ないと十分な分割を行えず、粗い推定になりやすいためと考えられます。
2点目に、推定時に与える交絡因子の設定についてです。
実践では交絡因子が未知であるケースも多く、モデル設計におけるWの選定は難しくなります。今回は、データ生成時に使われた交絡因子のみをWとして設定した場合と、他の変数も含めた場合とで比較しました。その結果、生成過程で使われた交絡因子のみを正しく設定した方が、推定精度は高くなりました。不要な変数をWに含めると、ノイズや過学習により逆に推定精度が下がると考えられます。この結果からWを多く含めればよいわけではないという示唆が得られました。
まとめ
本記事ではユーザーごとの施策効果を推定する手法の実用性に関する検証をご紹介しました。検証の結果、Causal Forest DMLが手法の中では最も汎用的である点がわかりました。また、サンプル数や施策効果が小さいケースでは、精緻に施策効果を評価することは難しいことがわかりました。これらの結果が、ユーザーごとの施策効果を分析してみたい方の参考になれば幸いです。
今後は今回の結果を深掘りするような検証を引き続き進めることで、より効果的な施策評価の実現を目指していきたいと考えています。また実際の施策に対しても既存の方法と並走しながら上記の手法の活用を進めていければと思っています。
ZOZOでは、一緒にサービスを作り上げてくれる方を募集中です。ご興味のある方は、以下のリンクからぜひご応募ください。
引用
因果推論 基礎から機械学習・時系列解析・因果探索を用いた意思決定のアプローチ
機械学習で因果推論 Double Machine Learning