
※AMP表示の場合、数式が正しく表示されません。数式を確認する場合は通常表示版をご覧ください
※2020年11月7日に、「Open Bandit Pipelineの使い方」の節に修正を加えました。修正では、パッケージの更新に伴って、実装例を新たなバージョンに対応させました。詳しくは対応するrelease noteをご確認ください。今後、データセット・パッケージ・論文などの更新情報はGoogle Groupにて随時周知する予定です。こちらも良ければフォローしてみてください。また新たに「国際会議ワークショップでの反応」という章を追記しました。
ZOZO研究所と共同研究をしている東京工業大学の齋藤優太です。普段は、反実仮想機械学習の理論と応用をつなぐような研究をしています。反実仮想機械学習に関しては、拙著のサーベイ記事をご覧ください。
本記事では、機械学習に基づいて作られた意思決定の性能をオフライン評価するためのOff-Policy Evaluation (OPE)を紹介します。またOPEを含めたバンディットにまつわる研究利用のためにZOZO研究所が公開したOpen Bandit Datasetと開発したパッケージOpen Bandit Pipelineの特徴や使い方を解説します。
なお、本記事はこちらのプレスリリースに関連する内容になっています。また本記事の内容は、先日arXivで公開した論文の内容を噛み砕いて日本語で紹介したものになっています。気になる方はぜひ元論文も参照してみてください。さらに、2020年8月27日にオンラインで開催されたCFML勉強会にて本記事の内容に関する発表を行っており、その際の発表資料も公開しています。この発表資料は、本記事の内容を補完するような例を紹介していたりするので、是非合わせてご覧ください。
モチベーション
機械学習は予測のための技術としてもてはやされています。実際多くの論文が、解く意味があるとされているタスクにおいてより良い予測精度を達成することを目指しています。もちろん予測値をそのまま活用する場面も多くあるでしょう。しかしとりわけウェブ産業における機械学習の応用場面に目を向けてみると、機械学習による予測値をそのまま使うのではなく、予測値に基づいて何かしらの意思決定を行っていることが多くあります。例えば、各ユーザーとアイテムのペアごとのクリック率を予測し、その予測値に基づいてユーザーごとにどのアイテムを推薦すべきか選択する。または、商品の購入確率予測に基づいてユーザーごとにどの商品の広告を提示するか決定する、などです。これらの例ではクリック率や購入確率の予測そのものよりもそれに基づいて作られる推薦や広告配信などの意思決定が重要です。
本記事の興味は、機械学習による予測値などに基づいて作られる意思決定policyの性能を評価することにあります。例えばクリック率の予測値に基づいてアイテム推薦の意思決定を行う場合、オフラインでクリック率の予測精度を評価指標としていることがあるでしょう。しかし、これは非直接的な評価方法です。予測値をそのままではなく何らかの意思決定を行うために用いているのならば、最終的に出来上がる意思決定policyの性能を直接評価するべきです。
意思決定policyの性能評価として理想的なのは、policyをサービスに実装してしまい興味があるKPIの挙動を見るというオンライン実験でしょう。しかし、何でもかんでもオンライン実験ができるわけではありません。なぜならば、オンライン実験には大きな実装コストが伴うからです。性能の悪い意思決定policyをオンライン実験してしまったときに、実験期間においてユーザー体験を害してしまったり、収入を減らしてしまう恐れもあります。従って、古い意思決定policyにより蓄積されたデータのみを用いて、新しい意思決定policyをオンラインに実装したときの性能を事前に見積もりたい、というモチベーションが生まれます。
このように、新たな意思決定policyの性能を過去の蓄積データを用いて推定する問題のことをOff-Policy Evaluation (OPE)と呼びます。NetflixやSpotify、Criteoなどの研究所がこぞってトップ国際会議でOPEに関する論文を発表しており、特にテック企業から大きな注目を集めています。正確なOPEは、多くの実務的メリットをもたらします。例えば、ある旧ロジックをそれとは異なる新ロジックに変えようと思ったとき、新ロジックがもたらすKPIの値を旧ロジックが蓄積したデータを用いて見積もることができます。また、ハイパーパラメータや機械学習アルゴリズムの組み合わせを変えることによって多数生成される意思決定policyの候補のうち、どれをオンライン実験に回すべきなのかを事前に絞り込むこともできます。
以降、OPEの一般的な定式化と標準的な推定量(手法)を紹介します。
Off-Policy Evaluationの定式化
ここでは、OPEの問題を定式化します。特徴量ベクトルを、取り得る
個の行動を
、観測される報酬を
とします。
は、潜在目的変数と呼ばれる因果推論で良く用いられる記法で、例えばある行動
を選択した時の報酬は
として表されます。ここで注意が必要なのが、
という行動を選択したならば、その行動に紐づく潜在目的変数
しか観測されないことです。それ以外の潜在目的変数の組
は分析者には観測されないということになります。これらの記号をイメージするための例を表1に示しました。
| 応用例 | 特徴量 |
行動 |
目的変数 |
|---|---|---|---|
| 映画推薦 | 年齢、性別、過去の映画視聴履歴など | 映画の種類 | クリック有無、視聴時間など |
| 投薬 | 年齢、性別、体重、過去の検査結果など | 薬の種類 | 生存有無、血糖値など |
さて、意思決定policy とは、特徴量から行動空間
上の確率分布への写像
として定義されます。つまり
は、ある
というベクトルで特徴付けられるデータに対して、
という行動を選択する確率です(つまり、
)。
は、まさにどんな状況でどの行動をとるべきかを司る意思決定policyと言えるでしょう。
ここである意思決定policy の性能を次のように定義します。
つまりは、
という意思決定policyを導入した際の目的変数の期待値です。例えば目的変数がクリック有無ならば、
は
によってもたらされるクリック率、ということになり、意思決定policyの性能の定義として妥当でしょう。
を実システムで一定期間走らせるオンライン実験ができるならば、その期間に観測される目的変数の平均をとることで困難なく
を推定できます。しかし、冒頭で説明したようにオンライン実験を行うこと自体に多くの困難が付きまといます。よってオンライン実験の代替案として、
の性能をオフライン評価することを考えてみましょう。オフライン評価のためのデータとして、過去の意思決定policy(旧ロジック)である
によって次のような
個のデータを含む
で表されるデータセットを蓄積していたとします。
なおなぜ過去のpolicyの添え字がなのかというと、このようなデータを集める際に走っていた過去のpolicyのことを論文では良くbehavior policyと呼ぶからです。一方で、これからオフラインで性能を評価したい新たなpolicyのことは counterfactual policyやevaluation policyと呼びます。
は、観測される特徴量ごとに過去の意思決定policyが
というふうに行動を選択し、それに紐づく潜在目的変数
が観測されることで構成されます。OPEは、過去のpolicyとは異なる新たな意思決定policy(新ロジック)
の真の性能である
を過去の蓄積データ
を用いて精度良く推定してくれる推定量
を作ることを目的とします。なお推定量
の理論的な性能は次のmean-squared-error (MSE)で評価されます。MSEが小さい推定量ほど、正確なオフライン評価を可能にしてくれるということです。

2つ目の等式はいわゆるbias-variance分解です。ここで、で
です。MSEの意味で良い推定精度を達成するためには、biasとvarianceの両方を考慮してあげる必要があります。次章で紹介する標準的な推定量は、ざっくりとbiasを抑えるのが得意なものとvarianceを抑えるのが得意なものに分けられます。bias抑制重視の推定量なのかvariance抑制重視の推定量なのかを理解しておくことは、場面ごとにどの推定量を用いるべきなのかを考える上で役に立ちます。
標準的な推定量
ここでは、意思決定policyの性能をオフライン評価するための標準的な方法として、Direct Method (DM)・Inverse Probability Weighting (IPW)・Doubly Robust (DR)という3つの推定量を紹介します。
Direct Method (DM)
DMはまず、過去に蓄積されたデータを使って特徴量から目的変数の期待値を推定するモデル
を得ます。
には、リッジ回帰やランダムフォレストなど良く知られた機械学習の手法が用いられます。次に、
を用いて次のように
の性能を推定します。
 つまり、DMは潜在目的変数を
つまり、DMは潜在目的変数をで置き換えてしまおうという発想だとわかります。もちろんDMの推定精度は、
の推定精度に大きく依存します。
が
を良く推定できていればそれを用いて出来上がる
も
を良く推定します。しかし、
の推定精度が悪ければ
のオフライン評価に失敗してしまいます。現実的な設定において、
を良く推定することは難しい場合が多いです。これらの点から、DMはMSEのうちbiasの部分が大きいという問題を抱えていることが知られています。一方で、varianceが問題になることはあまりありません。
Inverse Probability Weighting (IPW)
次に紹介するのは、DMとは全く異なる発想に基づくIPWという手法です。これは、過去の意思決定policyと評価したい新たな意思決定policyの行動選択確率の比で観測されている目的変数を重み付けることで、次のようにを推定します。

IPWはいくつかの妥当な仮定のもとで不偏性を持ちます。すなわち、MSEのうちbiasの部分が0ということです。一方で、データが少ない場合やと
が大きく異なる場合に、varianceが大きくなってしまう問題があります。つまり、DMとIPWの間にはbiasとvarianceのトレードオフがあるのです。基本的にデータが十分にあればIPWが望ましいですが、データが少ないときにはDMの方が良い推定精度を発揮することがあります。
Doubly Robust (DR)
DRはここまでに紹介したDMとIPWをうまく組み合わせた手法で、次のようにしての性能を推定します。

つまり、DRはDMによる推定値をベースラインとしつつも、第二項においてIPWのような方法によりDMが使っている目的変数の期待値のモデルの推定誤差を補正していることがわかります。このような賢い方法をとることにより、DRはIPWの不偏性を保ちつつ(多くの場合)varianceを減少できることが知られています。
まとめ
本章では、DM・IPW・DRというOPEにおいて標準的な推定量を簡単に紹介しました。これらの理論的性質やより発展的な推定量に関して詳しいことが知りたい方のために、本記事の最後にさらなる学習のための参考文献をまとめています。ここで紹介した基本となる3つの推定量さえきちんと理解しておけば、他のもう少し複雑な手法もそんなに悩むことなく理解できるはずです。
Off-Policy Evaluationの研究の課題
さて実はここからが本記事の本題です。ここまでOPEのモチベーションと標準的な推定量を簡単に紹介してきました。「早速使ってみたい」と思った方もいるかもしれません。事実、研究分野としてとても盛り上がっており、ここ数年で多くの理論的知見が得られています。しかし、OPEに関する論文で行われている実験に目を向けてみると、実は次のような課題があることに気が付きます。
- 理論系の論文では多クラス分類問題を無理やりOPEの設定とみなすなどの人工的で非現実的な実験が行われている
- 実証系の論文では実データを使う場合があるものの公開はされておらず、他の研究者による再現が不可能である
OPEに関する既存論文が採用している実験方法を表2にまとめました。私たちの知る限りOPEの実験を可能にする研究用公開実データは存在しません。もしご存知の方がいらっしゃったらぜひ連絡をください。
| OPEの実験方法 | その実験方法が取られている論文 |
|---|---|
| 多クラス分類問題を無理やりOPEの設定とみなすなどの人工的な方法 | [1-11] |
| 実データを使っているが非公開 | [12-16] |
さて現実的でかつ再現可能なOPEの実験評価を行うためには、次のような条件を満たす公開実データが必要になります。
- 複数の意思決定policyによって収集されたデータが収録されている
- データ収集に用いられた意思決定policyが何なのか公表されている
以上の条件が満たされていれば、後の章で示す方法によってOPEの実験評価を行うことができます。また追加で以下のような条件も満たされていると色々な設定での信頼度の高い実験が可能になるという意味で望ましいです。
- 大規模である(数千万レコード以上)
- 多くの意思決定policyによって収集されている
- 複数の目的変数が収録されている
もしこれらの条件を満たすデータを公開可能だという方がいらっしゃったら、論文とともに世に送り出すことによって学術的に大きな貢献になる可能性があるので、是非検討してみてください。
なおCriteoが2016年に公開している実データは一見OPEの実験が可能に見えますが、1つの意思決定policyによるデータしか含まれない、意思決定policyが何なのか公表されていないという点からOPEの実験に使うことはできません。もう少し新しいところではSpotifyも似たようなデータセットを公開しているようですが、これも1つの意思決定policyによるデータしか含まれないという理由によりOPEの実験に使うことはできません。
Open Bandit Datasetの公開
OPE研究の実験における課題を解決すべく私とZOZO研究所、Yale大学の成田悠輔氏らによる研究チームは、特にOPEの研究に適したOpen Bandit Datasetを公開しました。このデータセットは、株式会社ZOZOが運営する大規模ファッションECサイトZOZOTOWNで収集されたものです。同社は、ZOZOTOWNのトップページにおいて多腕バンディットアルゴリズムを用いて意思決定policyを構成し、数あるファッションアイテムの中からユーザーごとに適したアイテムを推薦しています。バンディットアルゴリズムによるファッションアイテム推薦の例を図1に示しました。
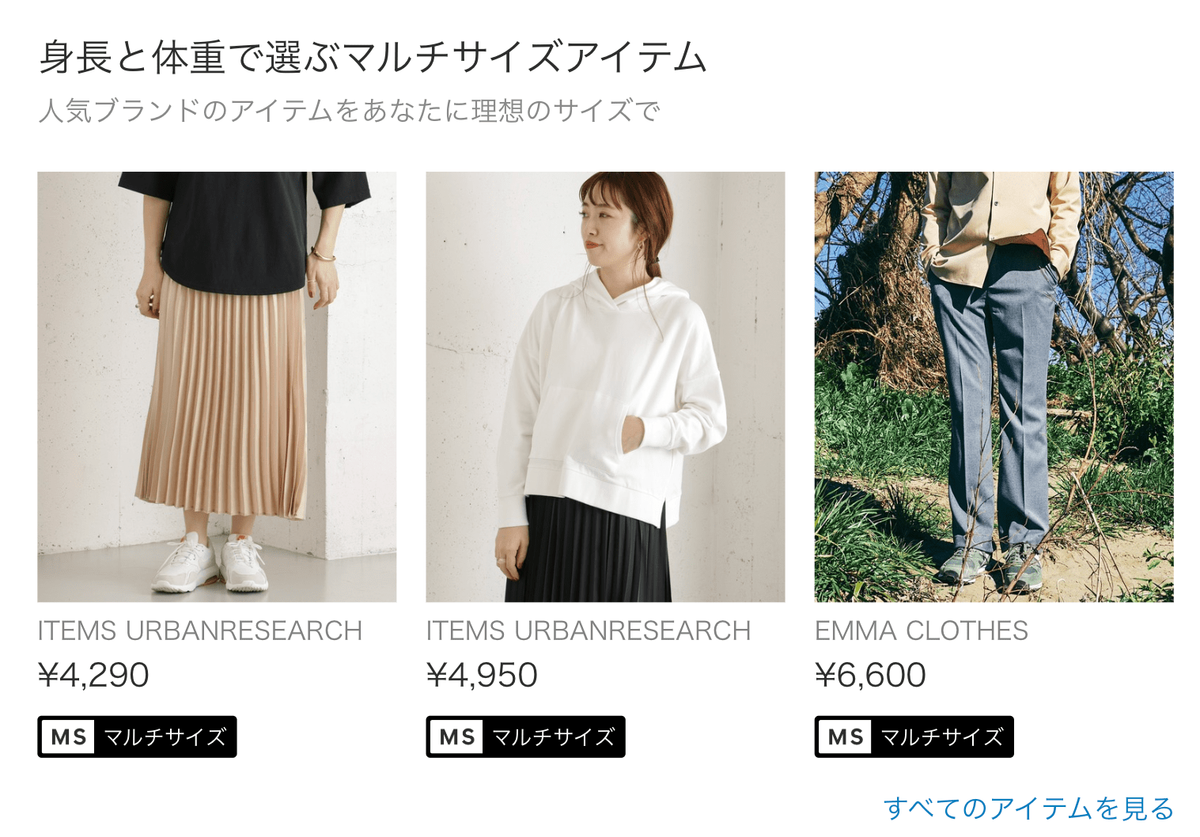
私たちは2019年11月下旬に7日間にわたる実験を行い、全アイテム(All)・男性用アイテム(Men's)・女性用アイテム(Women's)に対応する3つのキャンペーンでデータを収集しました。それぞれのキャンペーンでは、トップページ来訪ユーザーに対してRandomまたはBernoulli Thompson Sampling(BernoulliTS)という2種類の意思決定policyを確率的にランダムに選択して適用しています。表3はOpen Bandit Datasetの記述統計を示しています。
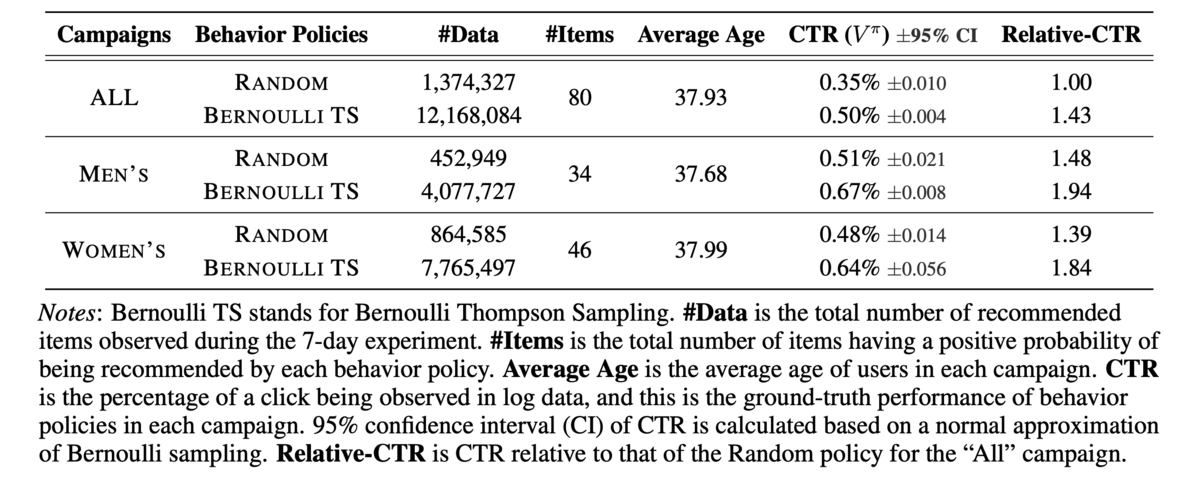
3つのキャンペーン(campaigns)と2つのbehavior policyごとに、データ数(#Data)・アイテム数(#Items:のこと)・クリック率(CTR:behavior policyの性能)などが記述されています。
1200万レコードを含む全アイテムキャンペーンとBernoulliTSの組み合わせを筆頭に、合計2600万レコード以上の大規模データセットとなっていることがわかります。
最後に、表4にOpen Bandit Datasetのイメージを示しました。各レコードは、推薦されたアイテムのid()、推薦位置、行動選択確率(
)、 クリック有無(
)、特徴量(
)で構成されています。なお推薦位置は、図1で示したZOZOTOWNにおけるファッションアイテムの推薦枠の3箇所の推薦位置のどこで推薦されたかを表しています(左から順に、1・2・3の値)。

少量のサンプルデータをこちらのディレクトリに置いているので、気になる方はチェックしてみてください。
Open Bandit Pipelineの公開
Open Bandit Pipelineの概要
さてOpen Bandit Datasetの公開だけでもOPEの研究を特に実験面からサポートするという意味で大きな貢献だと言えます。しかし我々の研究チームはデータセットに加えて、Open Bandit Pipeline (OBP) というバンディットアルゴリズムやOPEの性能評価のためのPythonパッケージを実装・公開しました。我々のOBPにより、研究者はOPE部分の実装に集中しつつ、再現性のある手順で他の手法との性能比較を行うことができるようになります。また機械学習エンジニアやデータサイエンティストなどの実践者は自社サービスにおいて旧ロジックが収集した過去のデータを使って簡単に新ロジックの性能を推定することが可能になります。図2にOBPの構成を記しました。

図に示したように、OBPは4つの主要モジュールで構成されています。datasetモジュールには、Open Bandit Dataset用のデータ読み込み用のクラスや人工データ生成のためのクラスを実装しています。policyモジュールには、バンディットアルゴリズムなどに基づいた意思決定policyを実装するためのインタフェースやいくつかの標準的なアルゴリズムを実装しています。simulatorモジュールには、オフラインで意思決定policyのシミュレーションを行うための関数を提供します。opeモジュールには、標準的なOPE推定量や新たな推定量を実装するためのインタフェースを実装しています。
OBPを活用することで、研究者は独自の意思決定policyやOPE推定量の実装に集中し、それらの性能を評価できます(図2の赤い部分)。 さらに実践者は、独自のデータセットをパイプラインと組み合わせることで、自社の設定・環境でOPEを用いた意思決定policyの性能評価を行うことができるのです。
OBPについての詳細はリポジトリやドキュメントをご覧ください。
github.com zr-obp.readthedocs.io
Open Bandit Pipelineの使い方
ここではOBPの基本的な使い方を紹介します。説明のために、「旧ロジックであるRandom policyが収集した過去データを用いて、新ロジックであるBernoulliTS policyの性能をオフライン評価する」という仮想的な分析例を用います。このようなオフライン評価は、OBPを使うと次のように実装できます。
>>> from obp.dataset import OpenBanditDataset >>> from obp.policy import BernoulliTS >>> from obp.ope import OffPolicyEvaluation, Inverse Probability Weighting as IPW # (1) データの読み込みと前処理 >>> dataset = OpenBanditDataset(behavior_policy='random', campaign='all') >>> bandit_feedback = dataset.obtain_batch_bandit_feedback() # (2) オフライン方策シミュレーション >>> evaluation_policy = BernoulliTS( n_actions=dataset.n_actions, len_list=dataset.len_list, is_zozotown_prior=True, campaign="all", random_state=12345 ) >>> action_dist = evaluation_policy.compute_batch_action_dist( n_sim=100000, n_rounds=bandit_feedback["n_rounds"] ) # (3) Off-Policy Evaluation >>> ope = OffPolicyEvaluation(bandit_feedback=bandit_feedback, ope_estimators=[IPW()]) >>> estimated_policy_value = ope.estimate_policy_values(action_dist=action_dist) # Randomに対するBernoulliTSの性能の改善率(相対クリック率) >>> relative_policy_value_of_bernoulli_ts = estimated_policy_value['ipw'] / bandit_feedback['reward'].mean() >>> print(relative_policy_value_of_bernoulli_ts) 1.198126...
以下、重要な要素について解説します。
まず最初にデータを読み込みます。ここではすでにOBPのdatasetモジュールに実装されているOpenBanditDatasetクラスを用いて、Open Bandit Datasetを読み込んでいます。
# 「全アイテムキャンペーン」においてRandom policyが集めたログデータを読み込む(これらは引数に設定) >>> dataset = OpenBanditDataset(behavior_policy='random', campaign='all') # 過去の意思決定policyによる蓄積データ`bandit feedback`を得る >>> bandit_feedback = dataset.obtain_batch_bandit_feedback() >>> print(bandit_feedback.keys()) dict_keys(['n_rounds', 'n_actions', 'action', 'position', 'reward', 'pscore', 'context', 'action_context'])
次にオフラインで意思決定policyのシミュレーションを行います。これは教師あり機械学習のモデルを評価する際に、一度検証用データに対して予測をかけることに対応します。
# 評価対象の意思決定policyとして、BernoulliTSを用いる >>> evaluation_policy = BernoulliTS( n_actions=dataset.n_actions, len_list=dataset.len_list, is_zozotown_prior=True, # ZOZOTOWN上での挙動を再現 campaign="all", random_state=12345 ) # シミュレーションにより、BernoulliTSによる行動選択確率を算出 >>> action_dist = evaluation_policy.compute_batch_action_dist( n_sim=100000, n_rounds=bandit_feedback["n_rounds"] )
is_zozotown_prior=Trueとすることにより、データ収集期間にZOZOTOWNの推薦枠で実際に稼働したBernoulliTSの挙動を再現できます。なお、is_zozotown_prior=Falseとすると、自ら設定した事前分布か無情報事前分布が反映されます。
最後に、BernoulliTSの性能のオフライン評価を行います。ここでは、opeモジュールに実装されているIPW推定量を使います。
# 算出されたBernoulliTSの行動選択確率に基づき、IPW推定量を用いて性能をオフライン評価する # OffPolicyEvaluationクラスには、過去の意思決定policyによる蓄積データとOPE推定量を渡す(複数設定可) >>> ope = OffPolicyEvaluation(bandit_feedback=bandit_feedback, ope_estimators=[IPW()]) >>> estimated_policy_value = ope.estimate_policy_values(action_dist=action_dist) # 設定されたOPE推定量ごとの推定値を含んだ辞書が出力される >>> print(estimated_policy_value) {'ipw': 0.004553...} # 最後に、新ロジック(BernoulliTS)の性能と旧ロジック(Random)の性能を比較する # 新ロジックの性能はOPEによる推定値を、Randomの性能はログデータの目的変数の平均で推定できる真の性能を用いる >>> relative_policy_value_of_bernoulli_ts = estimated_policy_value['ipw'] / bandit_feedback['reward'].mean() # 以上のOPEによって、BernoulliTSの性能はRandomの性能を19.81%上回ると推定された >>> print(relative_policy_value_of_bernoulli_ts) 1.198126...
以上の簡単な実装で、新旧の意思決定policyの性能を旧ロジックが蓄積したデータのみに基づいて比較できました。ここでの実装例だと、旧ロジックのRandomによる過去の蓄積データのみを用いて、新ロジックであるBernoulliTSの性能が旧ロジックのそれを19.81%上回るという評価を得ました。この結果に基づいて、新ロジックをいきなり実戦投入したり、大きな被害が出ないと踏んだ上で安心してオンライン実験に進んだりできるのです。
なおここで用いた簡易例はquickstart exampleとして、notebookで動かせるようになっているので確認してみてください。その他にも、人工データなどを用いた豊富な活用例も提供しており、すぐに手を動かしながらOBPの使い方を把握することが可能になっています。
是非、git clone https://github.com/st-tech/zr-obpしてから遊んでいただけたらと思います。
DatasetとPipelineを活用したOPEの実験評価
最後に、Open Bandit DatasetとOpen Bandit Pipelineの組み合わせによって、標準的なOPE推定量の性能評価(意思決定policyの性能のオフライン評価の正確さの評価)を行ってみます。このOPE推定量の実験評価が、データ公開とOBPの実装によって我々が可能にしたかったことになります。
Open Bandit Datasetを用いたOPEの評価方法
ここではOpen Bandit Datasetを用いてOPE推定量の性能評価を行うための手順を紹介します。準備のため、意思決定policyA(例えばRandom)によって収集されたデータを、意思決定policyB(例えばBernoulliTS)によって収集されたデータを
と表します。また意思決定policyAを
、意思決定policyBを
としておきます。
次のような手順をとることで、OPE推定量の正確さを評価することが可能です。
OPEの評価のための手順
と
の性能をそれぞれもう一方のpolicyが収集したデータをもとに推定する。すなわち、
の真の性能
を
で推定し、
の真の性能
を
で推定する。
と
の性能をそれぞれのpolicy自身が収集したデータを用いて推定し、これらを
と
の真の性能とみなす。すなわち、
を
で、
を
で代替する。これは、オンライン実験を行って
と
の性能を推定していることに相当するため、真の性能とみなすことに妥当性がある。
- OPEの評価指標を用いて
の正確さを評価する。ここでは次の relative estimation errorをOPEの実験的な評価指標として用いる。これが小さい推定量ほど、意思決定policyの性能の正確なオフライン評価ができているということになる。なお、AとBを入れ替えると
の性能を推定する場合のrelative estimation errorの定義式になる。

少々複雑な手順に見えますが、と
を交互に新旧ロジックとみなしてOPEを行うようなシミュレーションを行うことで推定量
の正確さを評価しています。上記のようなOPEの評価を行うためには、複数の意思決定policyによって収集されたデータが含まれており、かつ
や
をログデータ上で動作させる必要があるためそれらの意思決定policyが何なのか公表されていることが必要だということがわかります。我々のデータセットと実装は、このような現実的で再現可能なOPEの評価を可能にするのです。
DM・IPW・DRの性能比較
さて上述のOPE推定量の評価手順を用いて、標準的なOPE推定量であるDM・IPW・DRの推定性能評価を行ってみました。実験設定は以下の通りです。
- Randomをbehavior policy(旧ロジック)、BernoulliTSをcounterfactual policy(新ロジック)とみなして、BernoulliTSの性能を推定した際のオフライン評価の正確さを評価
- DMやDRに必要な機械学習モデル
には、ロジスティック回帰を使用
- 10個の異なるブートストラップサンプルによる結果を用いて、relative estimation errorの信頼区間を推定
得られた実験結果を表5に示しました。
| 全アイテム (All) | 男性向けアイテム (Men's) | 女性向けアイテム (Women's) | |
|---|---|---|---|
| DM | 0.2319 | 0.2150 | 0.2261 |
| IPW | 0.1147 | 0.1347 | 0.0788 |
| DR | 0.1181 | 0.1200 | 0.0786 |
ここではシンプルなロジスティック回帰を使ったこともあるのか、DMは一貫して悪い推定精度を示しました。一方で、IPWとDRはほとんど大きな差が見られませんでした。よってより実装が簡単なIPWでオフライン評価をするのが実務的には良さそうです。しかし、DRもDMと同様に機械学習モデルを用いているため、これを違うモデルに変更するとDRの推定が良くなる可能性もまだ残されています。サンプリングなどによってデータ数を意図的に変えてみたりbehavior policyとcounterfactual policyを入れ替えてみると異なる結果が得られるかもしれません。是非色々試してみてください。
ここで行ったOPE推定量の性能評価に用いた実装は、こちらのリポジトリに置いてあります。READMEには、relative estimation errorの信頼区間も含めた詳細な結果を記載しています。
国際会議ワークショップでの反応
本記事で紹介したデータ公開とパッケージ実装を含む研究プロジェクトはこれまでに、ICML2020 RealMLやRecSys2020 REVEALなど、トップ国際会議の関連ワークショップで口頭発表を行ってきました。
特に、2020年9月26日にオンライン開催されたRecSys2020併設のREVEAL workshopでは、AmazonやGoogle・Criteo・Microsoftなどで研究をされている界隈で有名な方々と並んで約200人の聴衆の前で30分間本研究プロジェクトの内容を口頭発表する機会に恵まれました。反応は以下の通り大変好評で、発表が終わった後Zoomのチャットに好意的なコメントが並んでいた時は、とても嬉しかったです。本研究の方向性が間違っていないことを専門家からの反応によって確かめることができたり、プロジェクトの内容を広く周知できたとても良い研究発表機会になりました。
twitter.com昨日、RecSys恒例のREVEAL WSにて、約200人の前で30分 live talkしました。発表自体が好評だっただけでなく、発表後に米トップ大の教授から直々に誘いを受けるなど反響がありました。オンライン学会でも入念に準備すれば十分チャンスや繋がりを掴めるようなので、あなどらず是非本気出していきましょう pic.twitter.com/MH869hxJvg
— usaito (@usait0) September 27, 2020
また学会後に執筆されたいくつかのブログ記事にて、Open Bandit DatasetやPipelineについて触れていただきました。界隈で大きな注目を浴びることに成功したので、これからもデータの拡大やパッケージの機能追加、及び国際会議での周知などに一層力を入れ、OPEの分野では知らぬものがいないオープンソースに成長させていくつもりです。
RecSys 2020: Highlights of a Special Conference
Similar to last year, the REVEAL workshop attracted the most attention with more than 900 participants being around. You should definitely check it out. There was also the release of Open Bandit Pipeline – a python library for bandit algorithms and off-policy evaluation that was considered as one of the highlights of this workshop.
-
REVEAL 2020: Bandit and Reinforcement Learning from User Interactions バンディットや強化学習に関するワークショップになります。NetflixやMicrosoftなどの企業から発表が多いです。日本からは、@usaitoさんのバンディットアルゴリズム用の大規模データセットの公開に関する発表があり、大きな注目を集めていました。
さいごに
本記事では、OPEと呼ばれる機械学習による予測ではなく意思決定policyの性能を直接評価する方法を紹介しました。またOPEの研究を 現実的で再現可能なものにするために我々が公開した大規模データセットと研究用パッケージについて紹介しました。今後もZOZOTOWNでの追加実装をもとにデータセットを増強したり、継続してパッケージのメンテナンスや機能追加を行っていくつもりですので、ぜひチェックしてみてください。
なお本記事の内容や元論文・データセット・パッケージに関しての質問、間違いの指摘、改善の提案などがありましたらメール (ZOZO研究所: zozo-research@zozo.com, 本記事の著者: saito.y.bj@m.titech.ac.jp)やTwitter (@usait0)でご連絡ください。
また、ZOZOテクノロジーズでは一緒にサービスを作り上げてくれる仲間を募集中です。ご興味のある方は、以下のリンクからぜひご応募ください!
さらなる学習のための資料
ここではOPEのことをもっと知りたい方のために、私自身がこれまで独学でOPEを勉強してきた際に活用してきた有用資料や論文をいくつか紹介します。
Doubly Robust Off-policy Evaluation with Shrinkage
ICML’19 Workshop on Real-world Sequential Decision MakingでのMicrosoft ResearchのMiro Dudík氏による招待講演。前半のOPEの導入が秀逸。OPEの定式化やDM・IPW・DRのなんとなくのイメージが沸いた方が視聴すると良い整理になるはず。バンディットと因果推論
CyberAgent、AI Lab 安井 翔太氏のCFML勉強会での発表資料。本記事では紹介を省いたOPEにおける困難や必要な仮定などが説明されており、眺めてみると良い勉強になるだろう。Contextual Bandits in Recommendation
元Spotifyで現Netflix ResearchのJames Mclnerney氏によるチュートリアル資料。推薦における利用の観点からcontextual bandit (意思決定policyを作る方法の一つ)から、そのオフライン評価に至までかなり詳細に解説されている資料。特に推薦システムにおけるOPEの利用を考えている方は眺めておいて損はないだろう。Off-policy Evaluation and Learning
Alekh Agarwal、Sham Kakade両氏によるワシントン大学での講義資料。本記事で紹介したDM・IPW・DRの理論的な基礎をきっちり把握したい方は目を通してみると良いだろう。Doubly Robust Policy Evaluation and Optimization
本記事で紹介した標準的な推定量であるDM・IPW・DRの理論的背景がまとまっているので、こちらもこれらの推定量の理論的な基礎を把握したい方は一読してみると良いだろう。Intrinsically Efficient, Stable, and Bounded Off-Policy Evaluation for Reinforcement Learning
Nathan Kallus・Masatoshi Uehara両氏によるNeurIPS'19論文。1章と2章においていくつかのOPE推定量の理論性質の比較がなされており、推定量のいろんな理論性質を知りたい方は楽しめると思う。
その他、もう少し発展的な推定量について知りたい方は[2,3,7,10,13,14]を企業による活用事例を知りたい方は応用系学会に出ている[12,15,16]あたりを読んでみると良いでしょう。
参考文献
Miroslav Dudík, Dumitru Erhan, John Langford, and Lihong Li. Doubly Robust Policy Evaluation and Optimization. Statistical Science, 29:485–511, 2014.
Yu-Xiang Wang, Alekh Agarwal, and Miroslav Dudik. Optimal and Adaptive Off-policy Evaluation in Contextual Bandits. In Proceedings of the 34th International Conference on Machine Learning, 3589–3597. 2017.
Mehrdad Farajtabar, Yinlam Chow, and Mohammad Ghavamzadeh. More Robust Doubly Robust Off-policy Evaluation. In Proceedings of the 35th International Conference on Machine Learning, 1447–1456. 2018.
Nathan Kallus and Masatoshi Uehara. Intrinsically Efficient, Stable, and Bounded Off-Policy Evaluation for Reinforcement Learning. In Advances in Neural Information Processing Systems. 2019.
Nikos Vlassis, Aurelien Bibaut, Maria Dimakopoulou, and Tony Jebara. On the design of estimators for bandit off-policy evaluation. In International Conference on Machine Learning, pages 6468–6476, 2019.
Cameron Voloshin, Hoang M Le, Nan Jiang, and Yisong Yue. Empirical study of off-policy policy evaluation for reinforcement learning. arXiv preprint arXiv:1911.06854, 2019.
Adith Swaminathan, Akshay Krishnamurthy, Alekh Agarwal, Miro Dudik, John Langford, Damien Jose, and Imed Zitouni. Off-policy Evaluation for Slate Recommendation. In Advances in Neural Information Processing Systems, pages 3635–3645, 2017.
Noveen Sachdeva, Yi Su, and Thorsten Joachims. Off-Policy Learning with Deficient Support. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), 2020.
Yi Su Pavithra Srinath Akshay Krishnamurthy. Adaptive Estimator Selection for Off-Policy Evaluation. In International Conference on Machine Learning, 2020.
Aman Agarwal, Soumya Basu, Tobias Schnabel, and Thorsten Joachims. Effective Evaluation Using Logged Bandit Feedback from Multiple Loggers. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), 2017.
Masahiro Kato, Masatoshi Uehara, and Shota Yasui. Off-Policy Evaluation and Learning for External Validity under a Covariate Shift. arXiv preprint arXiv:2002.11642, 2020.
James McInerney, Brian Brost, Praveen Chandar, Rishabh Mehrotra, and Ben Carterett, Counterfactual Evaluation of Slate Recommendations with Sequential Reward Interactions. arXiv preprint arXiv:2007.12986, 2020.
Yusuke Narita, Shota Yasui, and Kohei Yata. Off-policy Bandit and Reinforcement Learning. arXiv preprint arXiv:2002.08536, 2020.
Yusuke Narita, Shota Yasui, and Kohei Yata. Efficient counterfactual learning from bandit feedback. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 4634–4641, 2019.
Alexandre Gilotte, Clément Calauzènes, Thomas Nedelec, Alexandre Abraham, and Simon Dollé. Offline a/b testing for recommender systems. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, pages 198–206, 2018.
Alois Gruson, Praveen Chandar, Christophe Charbuillet, James McInerney, Samantha Hansen, Damien Tardieu, and Ben Carterette. Offline evaluation to make decisions about playlist recommendation algorithms. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, pages 420–428, 2019.
Damien Lefortier, Adith Swaminathan, Xiaotao Gu, Thorsten Joachims, and Maarten de Rijke. Large-scale validation of counterfactual learning methods: A test-bed. arXiv preprint arXiv:1612.00367, 2016.
Weihua Hu, Matthias Fey, Marinka Zitnik, Yuxiao Dong, Hongyu Ren, Bowen Liu, Michele Catasta, and Jure Leskovec. Open Graph Benchmark: Datasets for Machine Learning on Graphs. arXiv preprint arXiv:2005.00687, 2020.