
※AMP表示の場合、数式が正しく表示されません。数式を確認する場合は通常表示版をご覧ください
ZOZO Researchの斎藤です。私たちはファッションコーディネートの推薦や生成の基礎として、深層集合マッチングという技術を研究しています。本記事では、深層集合マッチングを理解する上で必要な諸概念の説明と、ファッションデータを使った実験結果について紹介します。対象読者としては、機械学習系のエンジニアや学生を想定しています。
集合マッチングとは
ある集合が与えられたとき、その集合にもっともマッチする集合を解の候補から選ぶという問題を考えます。
例えばコーディネートを画像集合として捉えると、あるコーディネートの一部分(部分コーデと呼びます)に対して合う部分コーデを選択するという問題設定を考えることができます。

このような問題を集合マッチングといいます。もちろん部分コーデではなく、後述するように複数のコーディネートを含めた集合を扱うことも可能です。
その他の応用例としても、ファッションとはまったく異なる分野で使えることが分かっており、例えば監視カメラ向けのタスクであるGroup Re-identificationと呼ばれる集団人物のマッチングにも適用できます(本記事では割愛します)。集合マッチングは将来性・拡張性の高いタスクといえそうです。
ここで、2つの部分コーデが合う(マッチする)かどうかを判定するには、部分コーデを構成するアイテム同士の調和性を調べることが重要になります。 しかし、どういったアイテム同士がどのようにマッチして結果的にコーディネートとして調和しているのかは、人間にとっても未知な場合が多いため、判別モデルや特徴量を人手で設計することは困難です。 そこで、強力な特徴学習(深層学習)の仕組みが必要になると考えられます。
また、集合は要素を入れ替えても不変なデータ構造であり、データの並べ方を考えなくてよいという性質を持っています。例えばコーディネートも同様に、アイテム同士を入れ替えても同じコーディネートです。 言い換えれば集合マッチングのタスクでは、このような集合データを取り扱うために、集合の性質を保つことができるモデルを構築しなければならないという難しさがあります。
コーディネートはもちろんのこと、集合を深層学習によってマッチさせる研究はこれまでにあまりなく、本記事ではこの技術を深層集合マッチングと呼びたいと思います。
部分コーデの教師データ作成
2つの部分コーデが合うかどうかを調べるモデルのパラメータを教師あり学習によって獲得することを考えます。どの部分コーデ同士がマッチするかをおおまかに人手でタグ付けすることは可能ですが、労力の問題から網羅的な教師データを用意できません。
そこで、 集合の再構成問題 を考えます。集合(部分コーデではなく完全なコーディネート)が与えられたとして、これを適当に2分割して共通部分のない部分集合(部分コーデ)を2つ作るとします。

このときモデルを通して、同じ集合から作られた2つの部分集合(部分コーデ)を正しく選べるか? を解くことにします。 もともと1つのコーディネートであったなら、そこから得られる部分コーデ同士は合うはずですから、そのペアを正例として扱います。
また、他のコーディネートを構成していた部分コーデ同士や、ランダムに選んだアイテムの集合は合わないと仮定して、そのような部分コーデの組み合わせは負例と考えることができます。
このようにして、アイテム同士がどのように合う/合わないかの情報は与えずに、部分コーデが“合う”という教師データを作ります。そして、アイテム同士が“合う”ときちんと認識することを通して、正しい部分コーデを選択できるモデルを特徴学習によって獲得することを狙います。
弊社では、IQONという日本の女性向けコーディネート投稿サービスを展開しておりましたので、こちらのデータを研究に用いました。
深層集合マッチング
深層集合マッチングは、特徴抽出レイヤーとマッチングレイヤーで構成されます。特徴抽出レイヤーをCross-Set Feature Transformation (CSeFT)、マッチングレイヤーをCross-Similarity (CS) 関数と呼びます。
例えば集合のペアが入力されたとき、マッチする度合いをCS(CSeFT(
))によって計算します。
特徴抽出してからマッチングスコアを計算するという順番でモデルが構成されます。
ここで、集合マッチングに必要なモデルの条件は、前述したように
- 集合内の要素を入れ替えても不変
- 2つの集合を入れ替えても不変
であることです。不変というのは、モデルの最終出力が変わらないということを意味します。後述するように、CSeFTとCS関数の合成関数はこの性質を満たすことが分かっています。
さらに、今回の集合マッチングでは異なる種類のアイテムを含む集合をマッチさせる必要があるため、元々まったく違う特徴ベクトル同士をマッチさせようとすることになりますから、簡単ではありません。マッチする集合同士ではよりマッチする特徴量を抽出し、そうでない場合はマッチしないと判定するに足る特徴量を抽出する必要があります。そのためには、何がマッチするかを集合間での相互作用(インタラクション)を通して抽出する枠組みが必要です。提案手法では、特徴抽出やマッチングの過程に集合間のインタラクションを導入して、表現力の高い特徴量を抽出できるようにしています。
特徴抽出
集合データといえども、その実体はコンピュータのハードウェア上では順番をもって格納されています。このデータの列を、集合の性質を保つように扱ったうえでインタラクションを考慮した特徴抽出をする必要があります。
特徴抽出器であるCross-Set Feature Transformation (CSeFT) レイヤーは、以下の式で構成されます。
ここで、は
番目のCSeFTレイヤーの処理によって得られた特徴ベクトルの列として表現されます(集合
の要素の特徴ベクトルを適当に並べたもの)。
は各画像に対して独立に適用した畳み込みニューラルネットワークから得られる特徴ベクトルの集合を指します。CSeFTは関数
によって構成されており、
は学習パラメータで2つの
の間でweight-sharingされています。なお、関数
は入力の第一引数の集合の要素の順番を保ったまま特徴抽出を行い、第二引数の集合の要素の順番には影響されないとします。これは第一引数に関しては置換同変、第二引数に関しては置換不変な性質を持っているといいます。この性質があれば、CSeFTは2つの集合内の要素に対して置換同変な関数となり、後述するように集合マッチングの条件を満たすことになります。
私たちは関数として以下の類似特徴ベースの変換を提案しています。ここでは例として、
番目のCSeFTレイヤーから抽出された集合
の
個目の要素の特徴量
を
に変換しています。
ここで、、
は線形関数で
、
はReLU、
です。
類似特徴ベース変換によって、似ている特徴ベクトル同士は似るように、似ていない特徴ベクトルはそのままになるように特徴写像を行います。
さらに、multiheadと呼ばれる構造を用いて、複数パターンの関数からの出力を用いることで、提案手法では精度を向上させています。
マッチング
前項で抽出した2つの特徴ベクトルの集合がマッチするかどうかを調べるために、本研究では以下のCross-Similarity (CS) 関数を用います。
ここでは、線形写像された2つの集合の各要素の間で非負の類似度の平均値を計算しています。さらにmultihead構造のように、CS関数の出力値を複数パターン計算してconcatenationしたのち、全結合層によって実数に変換して最終的なスコアとします。
なお、CSeFTは置換同変な関数、CS関数は置換不変な関数なので、それらの合成関数は集合内の要素について置換不変な性質を持ちます。また、集合を入れ替えても出力は不変です。これにより、集合マッチングの条件を満たすことが分かっています。
 -Pair-Set損失
-Pair-Set損失
提案手法では集合のペアに対してスコアを計算しますが、個別のペアに対して別々に負例を用意すると、大きな計算コスト(前処理)がかかります。そこで計算量が大きくなる問題を解くために、-Pair-Set損失を提案します。
-Pair-Set損失では、正例となる
個の集合ペア
を用意して、それぞれの正例ペアに対してその他のペアから
個の負例を作成することを考えます。つまり、ある集合
に対してマッチする可能性のある
個の候補
を用意します。このとき真の解は
で、他の候補は負例として考えます。この方法を用いることで、例えばTriplet損失よりも効率的に学習が可能になることが分かっています。

実験
ここでは例として冒頭に述べたようにコーディネートのマッチングを行います。
可視化
まず、提案手法で学習した結果をテストデータの集合を用いて可視化してみます。関数は入力の集合ペアの各要素の間でインタラクションの重みを計算していることを利用します。具体的には、関数
に関する式の
の部分は、集合
の
番目の要素に対する
の要素
からの重みといえそうです。また同様に、集合
の要素への
の要素からの重みも確認できます。この重みの値を正規化して可視化したものが下記の図です。


正しい集合ペアに関してはインタラクションの重みが多数得られており、誤った集合ペアに関してはスパースな結果になっていることが分かります。ここで、重みの値が0のときはインタラクションを示す矢印を表示していません。このようにインタラクションがスパースになると、最終的なマッチング度合いを示すスコアが低く現れる傾向になり、逆に強くインタラクションが複数得られるとスコアが高くなりうると考えられます。
定量評価
以降ではIQONのデータセットを用いて定量評価した結果を示します。提案手法を評価するタスクは (1) 部分コーデマッチングと (2) 複合コーデマッチングの2つです。
比較手法
比較手法としてSet TransformerとBERTを導入し、集合マッチング向けに拡張して用いることにします。Set Transformerは近年提案されたstate-of-the-artの集合関数で、BERTは言語タスクのstate-of-the-artです。Set Transformerの拡張では、集合ごとにSet Transformerによって特徴ベクトルを1つ抽出し、それらの内積を2つの集合のマッチ度合いとして定義します。BERTの拡張では、BERTの入力に2つの集合の和集合を用います。比較のためにBERTのpre-trainingは用いず、また個別のtoken embeddingは用いずに、segment embeddingのみ導入して内部的に2つの集合を区別します。Set Transformerの拡張では集合マッチングに必要な置換不変性は満たしますが、特徴抽出の過程で集合間のインタラクションは提供されません。BERTの拡張では集合間のインタラクションは提供されますが、置換不変ではないという性質があります。
| 手法 | 置換不変性 | インタラクション |
|---|---|---|
| Set Transformer | ||
| BERT | ||
| Cross-Affinity (ours) |
(1) 部分コーデマッチング
冒頭で述べたように、1つのコーディネートを分割して正しい部分コーデのペアを作成します。このとき、正しくない部分コーデの候補をランダムに3つ用意したとき、提案手法は正しい部分コーデを選べるか? を調べました。なお、負例のアイテムは正例のアイテムと同じカテゴリになるように制約を加えました(例えばトップスとボトムス)。この制約を実装するために、本実験ではTriplet損失を用いました。
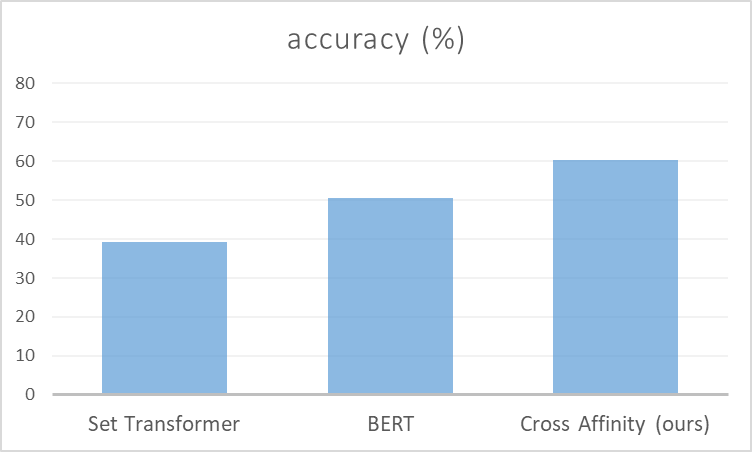
Set Transformer、BERT、提案手法の精度はそれぞれ39.2、50.5、60.2%でした。この結果から、提案手法が大きく勝っていることが分かります。
(2) 複合コーデマッチング
複合コーデマッチングでは、より複雑なデータに対応できるか調べるために、ランダムに選んだ4つの部分コーデの和集合(複合コーデ)をマッチングします。ランダムに選ぶので、複合コーデは様々なファッションスタイルの乱雑な混合を表現しています。こちらでは-Pair-Set損失を用いました。

このような集合でもうまくマッチングできれば、どのように複合的な趣向を備えているユーザに対しても対応できるモデルが原理的には学習できると考えられます。実験結果は以下の通りです。

Set Transformer、BERT、提案手法の精度はそれぞれ65.3、66.1、75.9%でした。提案手法が大幅に勝っていることが分かります。部分コーデを使用した際よりも全体的に精度が高くなっているのは興味深く、色々な考察が可能です。例えば集合に含まれるアイテムの数がある程度多くなれば、より識別に効くアイテムを含む確率が高まるため、精度向上を期待できます。しかしながら、ノイズのようなアイテムも同時に増えるはずであり、一概にはいえません。今後より深い検討が必要と考えられます。
結論
深層集合マッチングを提案し、ファッションデータで実験を行いました。近接するタスクでのstate-of-the-artの手法と比較し、提案手法は大幅に精度が高いことが確認できました。また可視化を通して、コーディネートの部分同士が“合う”とは何なのかを、結果的にモデルが学習しているという示唆を得ました。今後、私たちはこのモデルを継続的に発展させていく予定です。
謝辞
本記事に含まれる研究は、和歌山大学の八谷大岳先生、筆者の博士課程での指導教員である統計数理研究所の福水健次先生、弊所の中村拓磨氏の協力のもと行われました。
さいごに
本記事の内容はGroup Re-identificationへの応用も含めてMIRU2020で発表する予定です。ご興味のある方は口頭発表(ショート)をチェックしていただき、ぜひディスカッションしましょう!
また、ZOZOテクノロジーズでは一緒にサービスを作り上げてくれる仲間を募集中です。ご興味のある方は、以下のリンクからぜひご応募ください!