
こんにちは。ZOZO研究所の平川とML・データ部のデータサイエンスブロック2の荒木です。私たち2022年度の新卒入社メンバーは有志で社内マッチングアプリ「CLUB ZOZO」を運営しています。この記事では、興味関心が近い社員同士を自動でマッチングするアルゴリズムについてご紹介します。マッチング時のバッチ処理については推薦基盤ブロックの関口が解説していますので、興味のある方は併せてご覧ください。
目次
- 目次
- CLUB ZOZOとは
- CLUB ZOZOを運営するにあたり解決すべき課題
- ユーザ間の類似度を計るアプローチ
- 数理最適化を用いた偏りのないマッチング生成
- ダミーデータでの推論結果
- まとめ
- 最後に
CLUB ZOZOとは
CLUB ZOZOは、興味関心が近い社員同士をマッチングし、週に1回15分間のChat Timeをセッティングするサービスです。Chat Timeとは「上司」と「部下」の関係で実施される1on1ではなく、同じ興味関心を持つもの同士で純粋に会話を楽しんで欲しいという願いを込めて作った造語です。ユーザはSlackアプリ上で自分の興味関心を登録し(以下では「趣味タグ」と呼びます)待つだけでChat Timeがセッティングされるため、気軽に新しい仲間との出会いを楽しむことができます。
CLUB ZOZOは、新卒チーム開発研修で社内コミュニケーションを促進するためのツールを開発したことがきっかけとなり誕生したサービスです。2022年11月に社内リリースされ、2023年1月時点で約350名の社員が利用しています。
CLUB ZOZOを運営するにあたり解決すべき課題
CLUB ZOZOを運営する上でボトルネックとなるのがマッチングの生成です。サービスの性質上、以下の要件を満たす必要があるため手動での実施は運営側の負担が大きくなります。
- 共通の話題がある
- 同じ人とばかりマッチングしない
- マッチング機会が特定のユーザに偏らない
そこで、私たちは機械学習と数理最適化を組み合わせたマッチングアルゴリズムを開発し、CLUB ZOZOの運営コストを大幅に削減することに成功しました。開発したアルゴリズムは、「word2vecを用いた趣味タグの類似度計算」と「数理最適化を用いた偏りのないマッチング生成」の2つの工程から成ります。
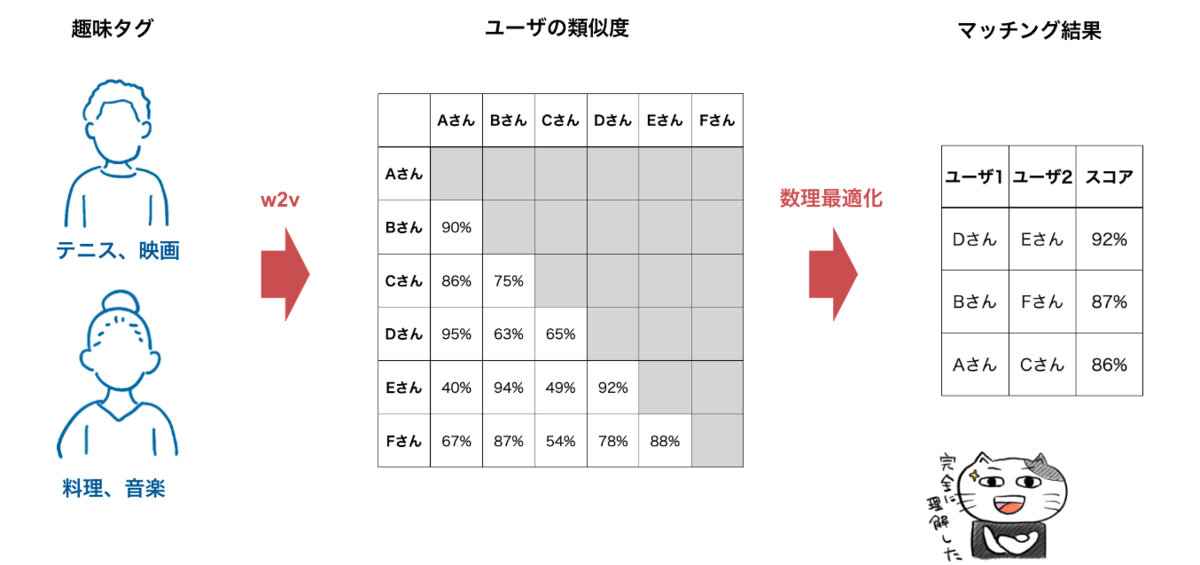
このアプローチは、ユーザのマッチング度合いに関する教師データが不要であるため、サービス立ち上げ段階で教師データが存在しない状況においても適用可能であるという利点があります。
以降では「ユーザ間の類似度を計るアプローチ」と「数理最適化を用いた偏りのないマッチング生成」について詳細を説明します。
ユーザ間の類似度を計るアプローチ
今回は、ユーザ間の類似度を「ユーザが登録しているタグの類似度」として計るアプローチを採用しました。具体的には、各ユーザのタグのすべてのペアに対して単語間の類似度を計算して、それを平均しています。
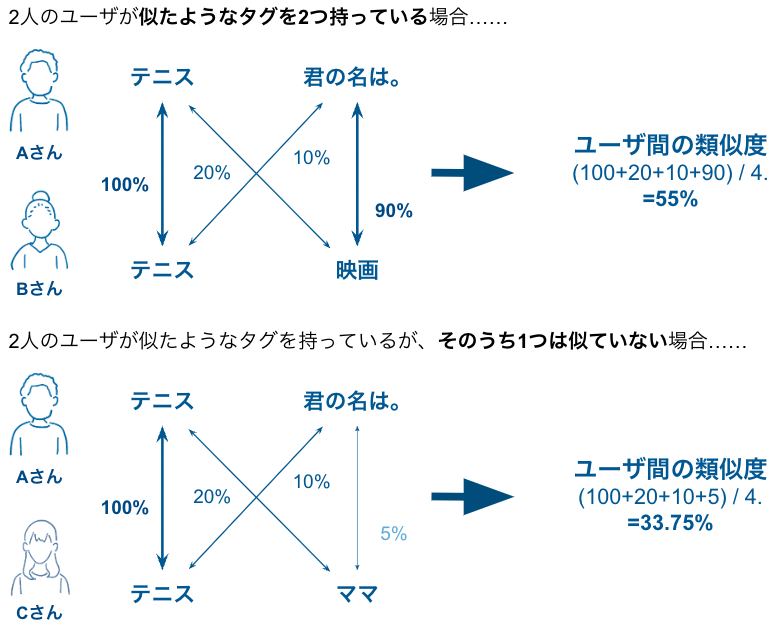
こちらの図の例では、以下の3名がそれぞれ次のタグを持っているとします。
- Aさん:テニス、君の名は。
- Bさん:テニス、映画
- Cさん:テニス、ママ
このとき、AさんとBさんは「テニス」という共通のタグを持っており、かつ「君の名は。」と「映画」という類似の趣味タグを持っているためユーザ間の類似度は55%となりました。一方で、AさんとCさんは「テニス」という共通の趣味タグを持っていますが、もう1つの「君の名は。」と「ママ」というタグはあまり似ていないためユーザ間の類似度は33.75%となります。つまり、AさんとBさんの方がより類似しているという直感をうまく反映できていると言えます。
また、単語間の類似度を計算する手法として「word2vec」を用います。word2vecは単語の意味をベクトルとして表現するモデルであり、自然言語を扱う機械学習モデルで広く用いられています。word2vecの学習には、Wikipediaが提供している全文データに対して、日本語用の形態素解析システムであるMeCabによる分かち書きを行ったデータを利用します。
しかし、このままでは辞書にない語句(=学習データに含まれない語句)や節はベクトル化できません。辞書にない語句や節の登録を禁止することも考えられますが、それではUX的にあまり嬉しくありません。そこで、もし趣味タグとして登録された文字列が辞書にない場合は、形態素解析で抽出した名詞のみを用いてベクトル化を行います。
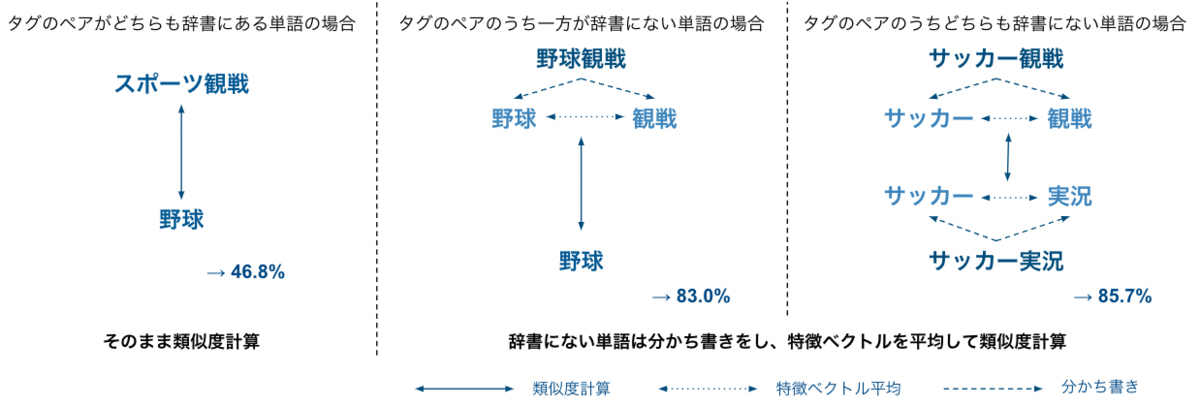
画像のように、辞書にない文字列のペアに対して類似度の計算を実現しています。例えば、「サッカー」と「スポーツ観戦」はどちらも辞書に存在するため、そのまま類似度を計算できます。一方で、「サッカー観戦」は辞書にないタグなので、一度分かち書きをして「サッカー」と「観戦」に分割します。そして、それぞれ「スポーツ観戦」とのスコアを計算し、その平均値を類似度とします。「サッカー観戦」と「サッカー実況」のようにタグのペアのうちどちらも辞書にない語句の場合は、それぞれ分かち書きを行い、各スコアを求めて平均した結果を類似度とします。
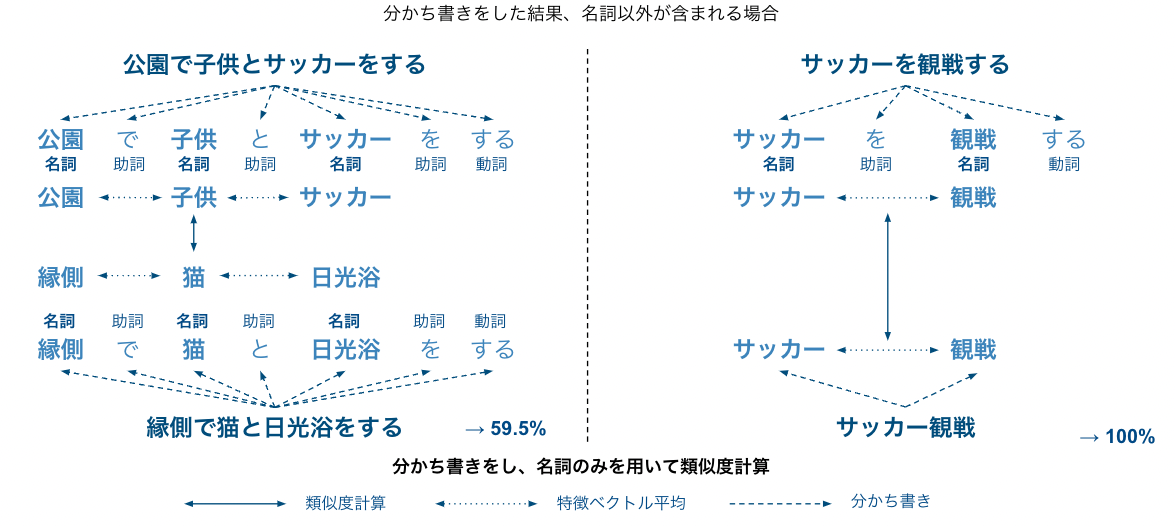
では、もしタグに少し長めの文章が入力された場合はどうなるのでしょうか。例えば「公園で子供とサッカーをする」と「縁側で猫と日光浴をする」というペアを考えてみましょう。分かち書きを行うと、それぞれ「公園・で・子供・と・サッカー・を・する」「縁側・で・猫・と・日光浴・を・する」になります。もし、このまま各単語のベクトルを平均して類似度を計算する場合、「で・と・を」といった助詞が類似度を底上げしてしまい不自然に高いスコアが出てしまいます。実際このペアの類似度は87.5%となります。そこで、今回は形態素解析をして、品詞が名詞である単語のみを用いてベクトルを平均します。名詞だけを用いる場合、今回のペアは59.5%となり少し低めに計算されました。また、「サッカーを観戦する」「サッカー観戦」という一見すると類似度が高めに出るはずのペアも、名詞以外を用いた場合は類似度が45.5%とかなり低めに計算されてしまいます。もちろん、名詞のみを用いた場合は100%となります。
ただし、分かち書きをしても単語が辞書に存在しない場合は、スコアを0%としています。この他にも、類似度が55%未満のタグのペアは経験的にあまりふさわしいペアでないことがわかっていますので、そのペアのスコアを0%にしてペアを無効化するなど細かな調整を入れています。
数理最適化を用いた偏りのないマッチング生成
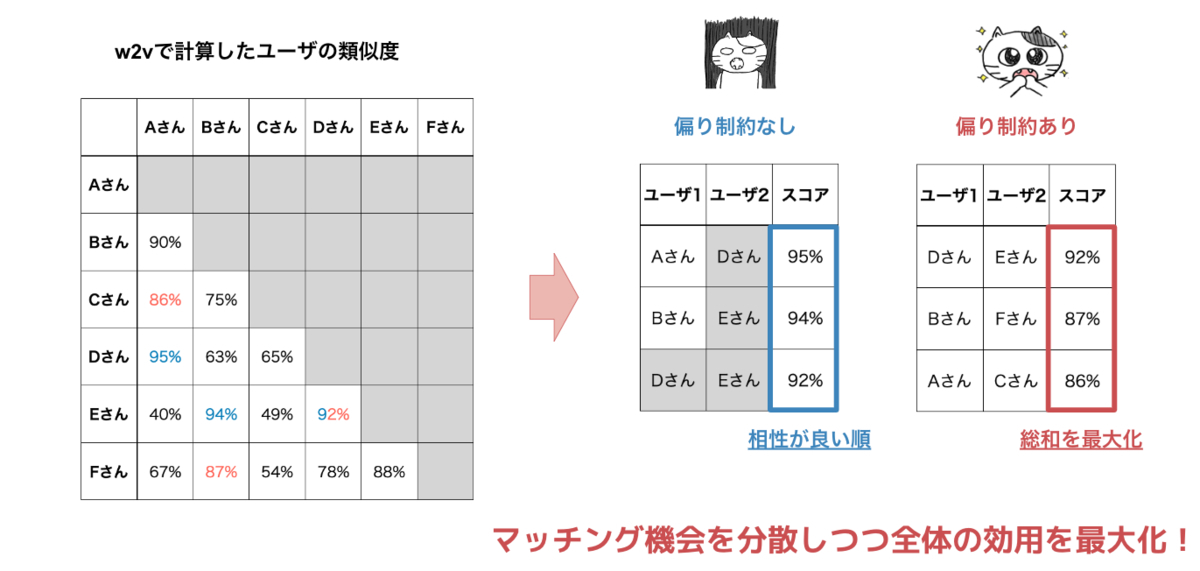
上記の方法で全ユーザの組に対してユーザの類似度が計算できたとします。ユーザの類似度が高いペアから貪欲にマッチングを成立させた場合(図の「偏り制約なし」)、「マッチング機会が特定のユーザに偏らない」という要件を満たさないマッチング結果になる場合があります。
別の方針として、一度のマッチング機会で各ユーザが1人のユーザとだけマッチングするという制約を満たしつつ、マッチングスコアの総和を最大化する解(図の「偏り制約あり」)を見つけるということが考えられます。
この問題は以下の数理最適化問題として定式化できます。
ここで、は生成するマッチング数、
はユーザ数、
は
番目のユーザと
番目のユーザの類似度、
は
番目のユーザと
番目のユーザがマッチングするか否かを表すバイナリ変数です(以下ではマッチング変数と呼びます)。この問題は「整数線型計画問題」と呼ばれるクラスの問題であり、PuLPなどの最適化ソルバーを用いて最適解を求めることができます。
この問題の最適化対象は、マッチングが成立した組のユーザ類似度の総和です。この値は全体の効用を表現しており、値が大きいほど良いマッチングを生成できていると考えられます。1つ目の制約条件は、生成するマッチング数が指定の数と一致することを保証するための条件です。例えば、を入力すると、10組のマッチングが生成されます。2つ目の制約条件は、一度のマッチング機会で各ユーザが1人のユーザのみとマッチングすることを保証するための条件です(以下では重複制約と呼びます)。全ユーザが同時に重複制約を満たす条件は、任意のユーザが重複制約を個別に満たすことと同値です。
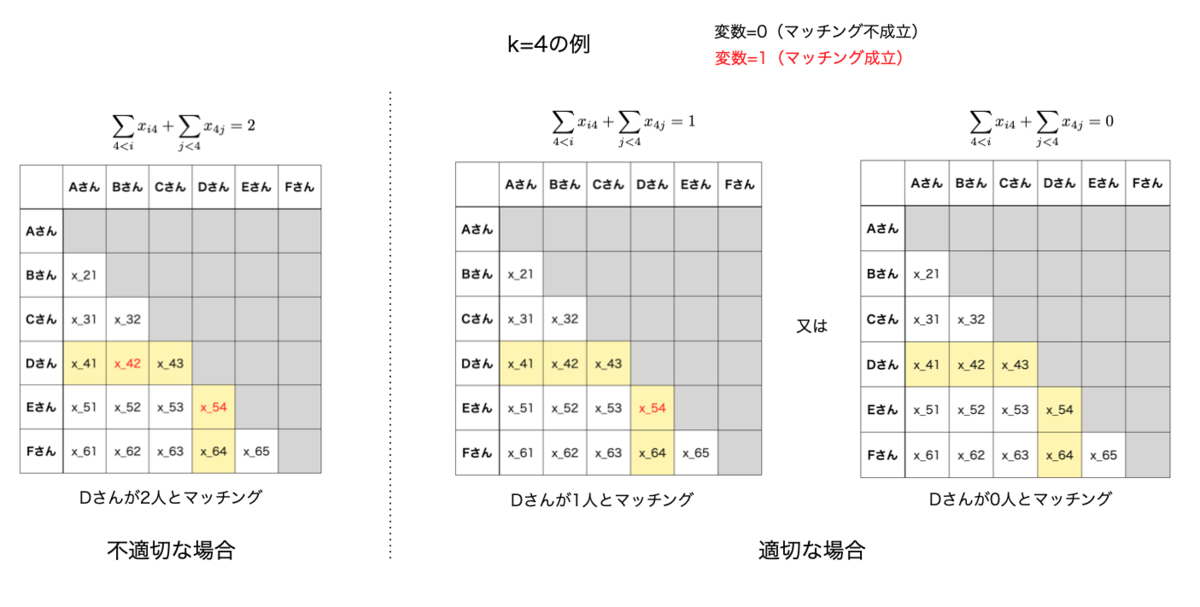
以下の図では、4番目のユーザ( / Dさん)に着目して重複制約の直感的なイメージを説明します。
のユーザがマッチングするか否かを決定する際に着目すべき領域は、図中の黄色に着色されたセル(以下では対象領域と呼びます)です。マッチング変数が赤色のセルはマッチング変数の値が1になり、黒色のセルはマッチング変数の値が0になることを表すものとします。この時、4番目のユーザが重複制約を満たすための条件は、対象領域に含まれるマッチング変数の中で値が1になるものが1個(DさんはEさんとだけマッチングする / 図の中央の例)もしくは0個(Dさんは誰ともマッチングしない / 図の右端の例)の場合に限ります。実際、図の左端の例のように対象領域に含まれるマッチング変数の中で値が1になるものが2つ以上存在する場合は、Dさんは2人以上のユーザとマッチングしてしまい不適となります。
さらに、運用上は重複制約に加えて、同じユーザとばかり連続でマッチングしない制約(以下では連続制約と呼びます)を加えることも重要です。連続制約については、上記の最適化問題をソルバーに入力する前段で、対応するユーザ同士のマッチングスコアに最低値である0を代入しておくことで達成できます。同様の原理を用いると、「部署指定マッチング」などの拘束条件付きマッチングについても実現できます。
ダミーデータでの推論結果
開発したアルゴリズムがうまくマッチングできるかを確認するために、ダミーのユーザデータを用いて実際にマッチングを行いました。
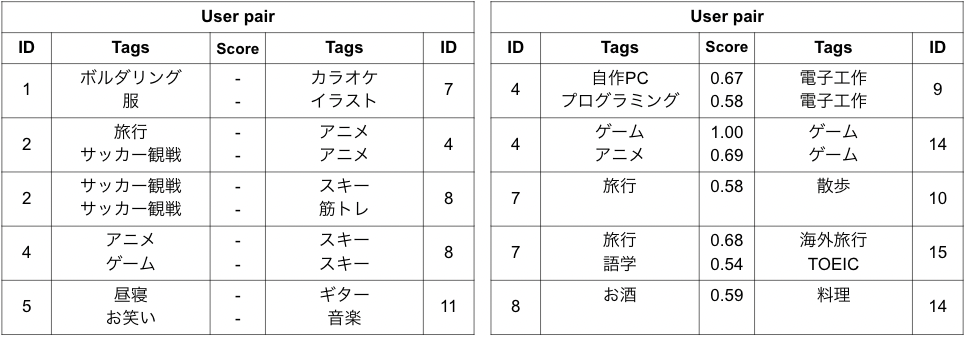
左側の表は完全にランダムでマッチングされた結果であり、ほとんどのペアが出鱈目で、良いマッチング結果とは言えません。対して右側の表はword2vecによるユーザの類似度を用いたマッチング結果であり、似ている趣味タグを持っているユーザ同士のマッチングを実現できたことがわかります。各表の中央にある「Score」は、各タグの類似度を示します。
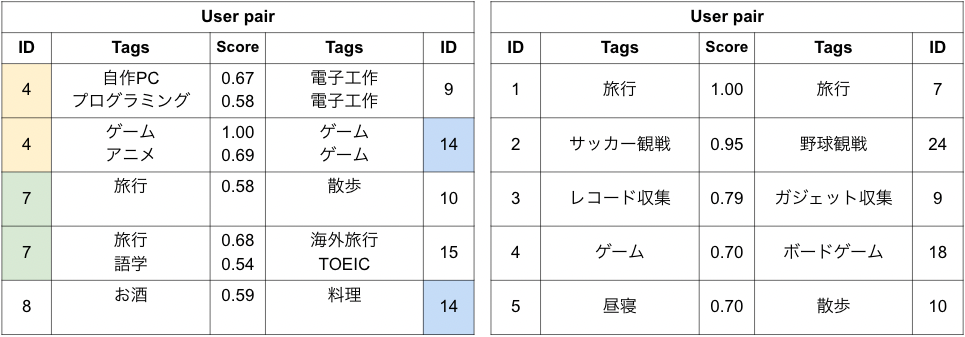
続いて、マッチングの偏りを抑止する制約の有無による結果の比較です。左側の表は先程のword2vecの結果と同じですが、同じユーザIDにそれぞれ色をつけています。ユーザID: 4, 7, 14のユーザがそれぞれ2回マッチングしており、ユーザに偏りができてしまっていることがわかります。対して右側の表はマッチングの偏りを抑止する制約を入れた結果であり、どのペアも必ず違うユーザが選ばれており、特定ユーザに偏らないマッチングを実現できたことがわかります。
まとめ
本記事では、新卒研修で開発した社内マッチングアプリ「CLUB ZOZO」のうち、ユーザ間のマッチングを行うアルゴリズムについてご紹介しました。word2vecと数理最適化の組み合わせで、興味・関心が近いユーザ同士を偏りなくマッチングするアルゴリズムを実現しました。今後は、実際にツールを利用している方から得られたフィードバックを教師データとして活用するほか、部署指定といった新機能の追加を考えています。
最後に
ZOZOではファッションに関する様々な分野で、研究や開発を一緒に進めていくデータサイエンティスト・MLエンジニアを募集しています。ご興味を持たれた方は、以下のリンクからぜひご応募ください。