
こんにちは。ML・データ部データサイエンス1ブロックの尾崎です。データサイエンス1ブロックでは機械学習モデルや、データ分析によって得られたルールベースのモデルの開発をしています。特に、ZOZOTOWNやWEARの画像データを扱っています。
本記事では、教師データがないPoC特有の「モデルの評価をどうするか」という課題への対策を商品画像の色抽出の事例とともに紹介します。教師データが無いという同じ境遇に置かれた方々の一助となれば幸いです。
目次
事業上の課題
アパレル商品の検索において、カラーは重要な要素の1つです。ZOZOTOWNでは15色のカラー(図1)を指定して検索できますが、より細かな粒度で商品を検索したいユースケースもあります。最近ではメイクやファッションにパーソナルカラーを取り入れることが流行しています。自分のパーソナルカラーに合う色で検索したいユーザもいることでしょう。ただ、現在のZOZOTOWNの検索だと「黄緑色」の商品に細かく絞り込みたくても、検索結果に「濃い緑色」の商品などが含まれてしまいます(図2)。


詳しいカラーで検索できる機能があるとUX向上にも寄与します。そのためには、これまでのカラーデータよりも詳細なカラーデータを得る必要があります。そこで、データサイエンス1ブロックでは教師データがない状況から、商品画像のカラーを抽出するモデルを開発しました。
どのようなモデルを作ったか
図3が、作ったモデルによる抽出・検索結果です。カラーコードの色で検索した結果を列ごとに表示しています。教師データがない状況でここまでの精度を出すことができました。

モデルの概要図は図4です。商品画像からカラーと比率を抽出するモデルです。

以下のステップでカラー抽出を実現しました。
- 商品画像からセマンティック・セグメンテーションによってファッションアイテムのマスクを抽出する
- 商品のカテゴリ情報から最適なマスクを選択する
- マスク内のピクセルのカラーをクラスタリングし、代表色にまとめる
カラーはL*a*b*(以下、簡単のためLabと表記する)色空間上の3次元のベクトルで表現しています。Lab色空間は人間の視覚に近くなるよう設計されており、人間が知覚する色差をユークリッド距離で表せます。
モデルの評価をどうしたか
教師データがないので、工夫して定量評価できるようにしました。定量評価をわざわざ行えるようにした理由は実験サイクルを早く、正確に回すためです。定性評価では実験のたびに関係者へ評価をお願いするので時間がかかりますし、評価に主観が入り込んでしまいます。
次の節からその工夫を解説します。主に正解ラベル、アノテーションを外注/内製するか、評価指標の決め方を紹介します。
何を正解ラベルとするか
教師データがなくても、定量評価には正解ラベルが必要です。正解ラベルは、商品画像に含まれる「カラーのみ」としました。他にも以下の表1の案がありました。

「カラーのみ」を選んだ理由はアノテーションコストが最も低く、かつ検索というユースケースにおいては「カラー」と「カラー数」が評価できれば十分だったからです。
アノテーションを外注するか、内製するか
今回は内製にしました。理由は「1件あたりのアノテーション時間」を計測し、最終的にかかる時間を見積もったところ、コア業務に支障がでない時間で終わりそうだったからです。この判断により、外注費用の節約ができましたし、アノテーションがまったく終わらないという事態も回避できました。
評価指標の設計をどうしたか
IoU (Intersection over Union) など、セマンティック・セグメンテーションの指標ではなく、評価指標を独自に定義する必要がありました。なぜなら、正解ラベルとして「ピクセル単位のラベル」ではなく、商品に含まれる「カラーのみ」を採用したからです。
まず、評価したい観点として以下の2つを洗い出しました。
- カラーが近いか?
- カラー数が同じか?
カラー数も評価する理由は今回のユースケースである検索において、どんなに色が近くても色数が異なればユーザ体験が損なわれると判断したからです。
この2つの観点を測るため、以下の図5のように色の近いペアごとに類似度を計算し、その和を正解と予測のうち多い方の色数で割った値を評価指標としました。
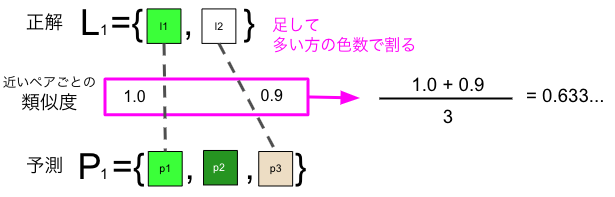
これを数式で表現すると以下になります。
:正解カラーの集合(
:Lab色空間上のベクトル)
:予測カラーの集合(
:Lab色空間上のベクトル)
:予測カラーと正解カラーの類似度(詳しい定義は後述)
なぜ、この式で2つの観点を測れるのかを解説していきます。まず、1つ目の観点である「カラーが近いか?」は、分子(類似度を足し合わせること)で測れます。ただし、近い色のペアのみに絞ります。なぜなら、すべてのペアだと以下の問題があるからです。
- 同系色間の類似度が強く反映されてしまう
- 近くない色のペアによって平均化されてしまう
例えば、以下の図6の左の類似度行列の予測には緑の同系色が含まれています。影の色を異なる同系色として抽出してしまうことがよくあります。こうなると白系のペア
と比べて、緑系のペア
の占める割合が高くなり、緑系が強く評価指標に反映されてしまいます。また、図6の左の方が右よりも上手く抽出できていますが、類似度の和は同じ3.3になってしまいます。これは、近くない色のペア
も含めているからです。
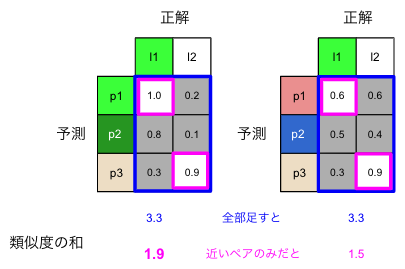
近い色のペアのみに絞ることで、緑は
のみが使われ、緑と白が対等に評価されます。また、左右の類似度の和は、それぞれ1.9、1.5となり「左の方が右よりも上手く抽出できている」ということを表せます。
の漸化式(以下に再掲)は、正解・予測カラーの集合から「近い色のペア=類似度が最大のペア」を順に取り出していくことを表しています。
:正解カラーの集合(
:Lab色空間上のベクトル)
:予測カラーの集合(
:Lab色空間上のベクトル)
この漸化式を図解したものが以下の図7になります。赤字が最も近いペアとして取り出されていきます。この赤字の類似度の和が分子になります。

ところで、類似度の定義は以下になります。
:予測・正解カラー間のユークリッド距離。Lab空間上の2点間のユークリッド距離は人間が知覚する色差に近しい1
:関係者間で定性的に決めた「これ以上離れたら、全く異なる色に感じる距離」。データセット内の距離の最大値を使ってしまうと、ほとんどの色のペアの類似度が高くなってしまうため。
わざわざ距離を類似度に変換した理由は、最終的な指標を「何色中、何色あってるか」と解釈しやすくするためです。例えば、2色のうち1色は完全一致(類似度1)、もう1色は半分くらい似ている色(類似度0.5)のとき「2色のうち1.5色あっている」と解釈できるようにするためです。
2つ目の観点である「カラー数が同じか?」は分母(正解と予測のうち、多い方の色数で割ること)によって測れます。他の案として類似度の平均にしてしまう、つまり、少ない方の色数
で割ってしまうと「カラー数が同じか?」を評価できません。例えば、正解が2色のとき、予測が2色でも100色でも分母は2となり同じ評価値になってしまいます。多い方の色数で割ることによって、100色より2色の方が良いことを表現できます。
以上より、今回の評価指標(以下に再掲)は、2つの観点「カラーが近いか?」と「カラー数が同じか?」を測れていると言えます。
最後に「予測の良し悪しと、評価値の良し悪しが連動するか」を具体的なデータで確認します。

図8の評価値が高い例では、カラーの近さとカラー数が両方とも合っています。一方、評価値が低い例では、全然違うカラーだったり、カラー数が間違っています。つまり、予測の良し悪しが評価値の良し悪しに連動していることを確認できました。このように評価値が高い/低い例を確認することで、評価指標に欠陥がないかを確認できます。この確認のおかげで「近い色のペアのみに絞る」や「多い方の色数で割る」という改善を思いつくことができました。
まとめ
本記事では、教師データがないPoC特有の「モデルの評価をどうするか」という課題に対して、商品画像の色抽出の事例とともに以下の解決策を紹介しました。
- 教師データが無くても、正解ラベルを用意して定量評価の方法を確立することで、実験サイクルを早く・正確に回せるようにしました。
- アノテーションの外注か内製かを選ぶにあたり「1件あたりのアノテーション時間」を計測し、最終的にかかる時間を見積もりました。この判断により、外注費用の節約ができましたし、アノテーションがまったく終わらないという事態も回避できました。
- 独自の評価指標や正解ラベルを定義する際は「ユースケースに必要十分な評価観点を明らかにすること」と「予測の良し悪しと、指標の良し悪しが連動するかを具体的なデータで確認すること」で適切な定量評価方法を設計できました。
ZOZOではデータサイエンティスト・MLエンジニアのメンバーを募集しています。今回紹介した画像タスクに興味ある方はもちろん、幅広い分野で一緒に研究や開発を進めていけるメンバーも募集しています。ご興味のある方は、以下のリンクからぜひご応募ください。
参考
- Jain, Anil K. (1989). Fundamentals of Digital Image Processing. New Jersey, United States of America: Prentice Hall. pp. 68, 71, 73. ISBN 0-13-336165-9.↩