
こんにちは。検索基盤部の橘です。検索基盤部では、ZOZOTOWNのおすすめ順検索の品質向上を目指し、機械学習モデル等を活用しフィルタリングやリランキングによる検索結果の並び順の改善に取り組んでいます。
最近行った並び順の精度改善の取り組みについては以下の記事をご参照ください。
また、検索基盤部では新しい改善や機能を導入する前に、A/Bテストを行い効果を評価しています。A/Bテストの内容や分析の自動化への取り組みについては以下の記事をご覧ください。
検索基盤部ではA/Bテストの事前評価として、オフラインの定量評価と定性評価を実施しています。特に定量評価は、並び順の精度改善の仮説検証を迅速に行う手段として有効です。
しかし、ZOZOTOWNのおすすめ順検索の商品ランキングロジックの1つであるフィルタリング処理についてはこれまで明確な定量評価の指標がなく、評価が難しく改善を進めることが困難な状況でした。本記事では、この課題に焦点を当て、特に定量評価の指標を決定するアプローチについて詳細に記載していきます。
目次
ZOZOTOWNのおすすめ順検索の商品ランキングロジックにおけるフィルタリング処理
ZOZOTOWNのおすすめ順検索の商品のランキングロジックは2つのフェーズに分けられています。
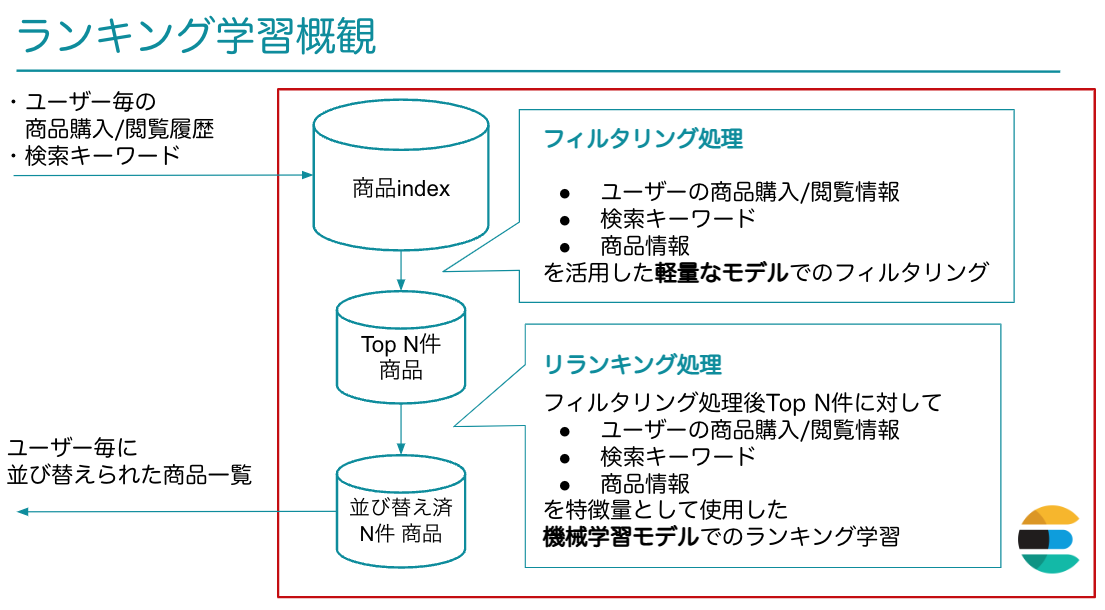
- フィルタリング処理:再現率を高めることを目的にルールベースのロジックや軽量な機械学習モデルを用いて商品のフィルタリングを行います。
- リランキング処理:フィルタ時のスコア結果トップN件に絞って「ランキング学習」と呼ばれる手法の機械学習モデルを用いた並び替え処理を行なっています。
以上のリランキング処理された並び順を検索結果に使用しています。
フィルタリング処理によりどのような商品群がリランキングされるのかが決まるので、フィルタリングの精度は最終的な検索結果に大きく影響を及ぼすことがわかります。続いて、このフィルタリング処理の精度の定量評価について記載していきます。
フィルタリング処理における定量評価
A/Bテストにおける定量評価の位置付けと目的
以下にA/Bテスト実施までのフローを示します。

定量評価及び定性評価は、事前評価としてA/Bテストの前に実施します。
事前評価を実施する目的として、以下が挙げられます。
- 『不要なA/Bテスト施策の排除』:A/Bテストは社内の人的リソースを多く必要とします。明確に改善効果がない、または悪化する可能性がある施策をA/Bテスト前に排除することで、リソースの無駄を防ぎます。
- 『リスクの低減』:致命的なエラーをA/Bテスト前に回避します。
- 『施策の内容理解』:関係者が施策の内容や意図をより深く理解できるようにします。
この記事で取り上げる定量評価は主に1の不要なA/Bテスト施策の排除を目的としています。以下では、その精度の改善効果を確認するための評価方法や指標について詳細に記載していきます。
検索結果の並び順のロジックを定量評価するには
検索エンジンは、入力された検索キーワードに対して組み込まれたロジックに基づき商品を並び替えて出力します。定量評価では、入力された検索キーワードに対する新旧ロジックの検索結果の並び順を比較することによって新旧ロジックの良し悪しを評価・判断します。
以下に「リバーシブルパーカー」で検索した場合の新旧ロジックの比較イメージを示します。

導入した評価指標
フィルタリング処理における『良い検索結果の並び順のロジック』は、具体的に何が期待されるのでしょうか?
一般的な検索結果の並び順のロジックの良し悪しを評価する手法として、過去のユーザー行動ログを基に「正解データ」を作成し、その正解データとロジックの検索結果を比較してnDCGなどの指標で評価します。
しかし、ランキングの指標をそのままフィルタリング処理の評価指標として用いるのは必ずしも適切とは言えません。フィルタリング処理に関しては以下2点を考慮する必要があります。
- 正解データは旧ロジックによる検索結果が基になっていることにより、旧ロジックの精度が過大評価される可能性(historical bias)がある。
- フィルタリング処理の検索結果は後のリランキング処理により並び替えられるので、正解データでフィルタリング処理時点での並び順の良し悪しを評価する必要性は低い。
これらの点を踏まえ、フィルタリング処理における良い検索結果の並び順のロジックを新ロジックは旧ロジックの精度を保ちつつ、旧ロジックとは明確な差異を持ち、異なる商品を数多く表示できるものと定義しました。
以上の定義を基に、以下の3つが確認できるような定量評価の指標を導入しました。
- 『精度の維持度』:新ロジックは旧ロジックと同等の(もしくはそれ以上の)精度を有しているか。
- 『多様性度』:新ロジックが、旧ロジックとは異なる商品を多く表示できるか。
- 『類似度』:新ロジックと旧ロジックの検索結果の並び順がどの程度類似しているか。
以下にそれぞれの評価指標について詳細に説明していきます。
『精度の維持度』の評価指標について
精度の維持度の指標としてコンバージョンカバー率を導入しました。具体的には、新旧ロジック検索結果の上位N件の商品の過去のコンバージョン数を比較し、新ロジックが旧ロジックの数値をどれだけカバーしているかを割合で表します。
※検索結果の上位N件は後のリランキング処理で並び替えを行う件数に該当します。
コンバージョンカバー率をベン図の部分で表すと以下のようになります。
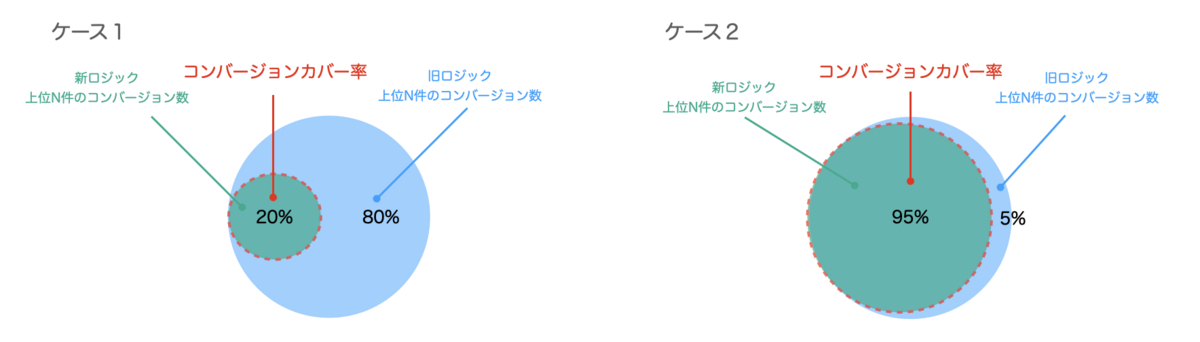
本指標を使ってどのように新ロジックの良し悪しを判断するかを説明します。
- ケース1ではコンバージョンカバー率が20%となっています。これは新ロジックの検索結果の上位N件のコンバージョン数が旧ロジックのそれの20%しかカバーしていないことを意味します。
- ケース2ではコンバージョンカバー率が95%となっています。これは新ロジックの検索結果の上位N件のコンバージョン数が旧ロジックのそれの95%をカバーしていることを意味します。
ケース2はケース1と比較しコンバージョンカバー率が大きいので、新ロジックの検索結果の上位に過去ユーザーにとってコンバージョンしやすい商品が多く含まれていると解釈できます。つまり、コンバージョンカバー率が大きいほど新ロジックは旧ロジックと同等の検索精度を持っていると期待できます。
『多様性度』の評価指標について
もし新ロジックの精度が旧ロジックの精度を維持していたとしても、新旧ロジックの検索結果が殆ど同等だった場合はA/Bテストをする必要性は低くなってしまいます。このようなロジックを除外できるように、旧ロジックとは異なる新しい検索結果をどれだけ取り入れているのかの指標が必要です。
これを踏まえ、多様性度の指標として新表示商品率を導入しました。具体的には、新ロジックで検索結果の上位N件に表示された商品の中で、旧ロジックで検索結果の上位N件に表示されない商品の割合で表します。
該当部分をベン図の部分で表すと以下のようになります。
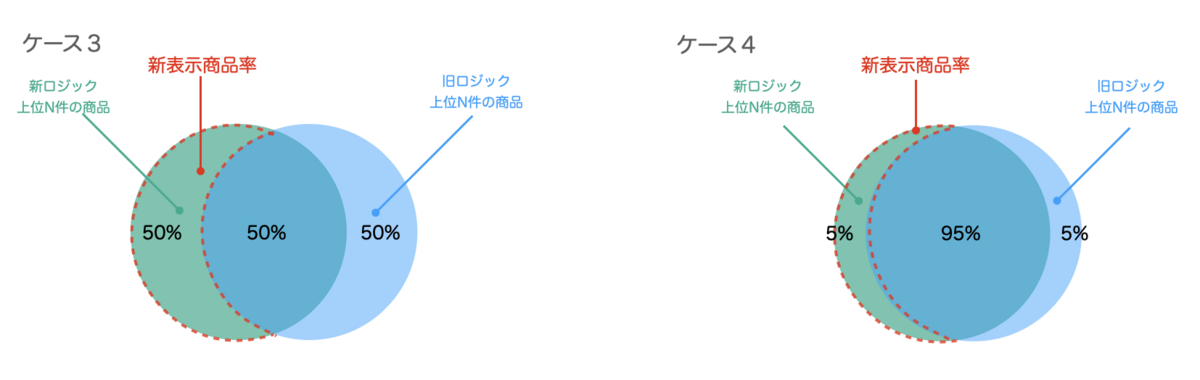
先ほどの指標を使ってどのように新ロジックの良し悪しを判断するかを説明します。
- ケース3では新表示商品率が50%になっています。これは新ロジックが旧ロジックに比べて新しい検索結果を50%も増やせていることを意味します。
- ケース4では新表示商品率が5%になっています。これは新ロジックが旧ロジックに比べて新しい検索結果を5%しか増やせていないことを意味します。
ケース3はケース4と比較し新表示商品率が大きいので、新ロジックの検索結果の上位には旧ロジックとは異なる新しい検索結果が多く含まれていると解釈できます。
『類似性』の評価指標について
『多様性度』と同様に、新旧ロジックで検索結果の並び順がほぼ類似している場合、A/Bテストをする必要性は低くなってしまいます。このようなロジックも除外できるようにする必要があります。
検索結果の並び順の類似性を評価する際の代表的な指標としてスピアマンの順位相関係数、ケンドールの順位相関係数、RBO(rank biased overlap)などがあります。
指標を選定する際、おすすめ順検索のフィルタリング処理における検索結果の並び順は「2つの検索結果の並び順は互いに含まれていない商品を含んでいる場合がある」点を考慮する必要がありました。
以上を考慮する場合、RBOは使うことができますが、スピアマンの順位相関係数とケンドールの順位相関係数は扱いが難しいです。
以下にコードを踏まえながら、上記の難点を説明します。
ケンドールの順位相関係数の難点
まず、ケンドールの順位相関係数を挙げて上記の難点について説明します。ケンドールの基本的な説明や算出方法はWikipediaの内容をご参照ください。
簡単なPythonコードでケンドールの順位相関係数の計算例を示します。ここではscipyのkendalltauライブラリを使います。
以下は両リストが同じ商品を含む場合のコードです。
!pip install scipy import numpy as np from scipy.stats import kendalltau # 2つの検索結果の並び順 search_result_1 = ['商品A', '商品B', '商品C', '商品D', '商品E'] search_result_2 = ['商品A', '商品B', '商品E', '商品C', '商品D'] # 2つの検索結果に含まれる商品をリスト化 all_goods = sorted(list(set(search_result_1 + search_result_2))) # 商品リスト内の商品に対して並び順の順位をつける関数 def assign_ranks(results, all_contents): return [results.index(c) for c in all_contents] ranked_1 = assign_ranks(search_result_1,all_goods) ranked_2 = assign_ranks(search_result_2,all_goods) # ケンドールの順位相関係数を計算 tau, _ = kendalltau(ranked_1, ranked_2) # 結果を出力 print("Kendall's tau:", tau) >> Kendall's tau: 0.6
ケンドールの順位相関係数をこのような場合に適用するときは、検索結果の並び順を基に商品リスト内の商品に対して並び順の順位をつけるようにし、それらを入力とし値を計算します。ケンドールの順位相関係数の値は-1から1の値をとり、値が低いほど負の相関、値が高いほど正の相関が高いことを示します。
この例の場合ケンドールの順位相関係数の値は0.6となります。
次に、異なる商品を含む場合のコードです。
search_result_1 = ['商品A', '商品B', '商品C', '商品D', '商品hoge'] search_result_2 = ['商品A', '商品B', '商品fuga', '商品C', '商品D']
商品hogeと商品fugaという両リストに異なる商品が含まれています。この場合、これらの商品の順位をどのように扱えば良いのかという問題があります。
一般的には、含まれていない商品を無視する意図で順位をNaNに置き換える方法があります。
def assign_ranks(results, all_contents): return [results.index(c) if c in results else np.nan for c in all_contents]
NaNを含む順位のデータを扱う場合、kendalltauの引数nan_policyを'omit'にすることで順位のデータ中のNaNを無視できます。
tau, _ = kendalltau(ranked_1, ranked_2, nan_policy = 'omit') print("Kendall's tau:", tau) >> Kendall's tau: 1.0
しかし、この場合のケンドールの順位相関係数の値は1.0と出力されてしまい、先ほどの互いに同じ商品を含んだ場合と比較しても違和感のある結果となってしまいます。
他にも様々な前処理方法が考えられますが、前処理方法により出力の値が変わってしまいます。よって、ケンドールの順位相関係数は、2つの検索結果の並び順において両リストに異なる商品を含んでいる場合に扱いが難しいと分かります。
RBO(rank biased overlap)
続いて、RBOを用いた場合について説明します。
RBOの値は0から1の値をとり、値が高いほど互いの並び順が類似していることを示します。RBOの特徴として、2つの検索結果の並び順の上位の商品が異なっていた場合に値を大きく減衰させます。
一般的に検索結果の並び順は上位の商品がより重視されるので、検索結果の並び順における類似性の評価指標として採用しやすい指標といえます。
RBOについての詳細はこれに関する論文であるA Similarity Measure for Indefinite Rankingsをご参照ください。
簡単なPythonコードでRBOの計算例を示します。ここではrboライブラリを使います。
以下は2つの検索結果の並び順が互いに同じ商品を含んだ場合です。
!pip install rbo import rbo # 2つの検索結果の並び順 search_result_1 = ['商品A', '商品B', '商品C', '商品D', '商品E'] search_result_2 = ['商品A', '商品B', '商品E', '商品C', '商品D'] # RBOを計算する value_rbo = rbo.RankingSimilarity(search_result_1, search_result_2).rbo() print("RBO:", value_rbo) >> RBO: 0.88
この例の場合、RBOの値は0.88となります。
次に、互いに含まれていない商品が存在する場合です。
search_result_1 = ['商品A', '商品B', '商品C', '商品D', '商品hoge'] search_result_2 = ['商品A', '商品B', '商品fuga', '商品C', '商品D'] ... print("RBO:", value_rbo) >> RBO: 0.41
この例の場合、RBOの値は0.41となります。互いに同じ商品を含んだ場合と比較し値が低くなっているので違和感のない値になっています。
RBOは互いの並び順にあるリスト内の共通商品数をベースに算出する手法のため、互いに含まれていない商品が存在する場合でも違和感のない結果を出すことができます。
以上を踏まえて『類似性』の評価の指標としてはRBOを導入しました。
まとめ
本記事ではZOZOTOWNのおすすめ順検索の精度改善における定量評価及びその指標決定のアプローチを紹介しました。定量評価の指標が整ったことで、A/Bテスト前に精度改善の検証が迅速にできるようになり、よりA/Bテストの実施頻度の向上が期待されます。
今後は施策を重ねていく中で、これまで紹介した指標のブラッシュアップや新規指標を追加していく予定です。また、A/Bテストの負担軽減のため、これらの指標値をより迅速に算出できるような仕組みの構築も進めていく必要があります。
おわりに
ZOZOでは、一緒にサービスを作り上げてくれる方を募集中です。ご興味のある方は、以下のリンクからぜひご応募ください。