
はじめに
こんにちは。ZOZO Researchの千代(@ryskchy)です。普段は主に数理最適化の技術を使った業務改善のための研究開発をしています。
ZOZOでは2022年から数理最適化の技術を使って最適な梱包資材を選ぶための取り組みを行なっています。本記事では梱包資材の選択のために解いている最適化モデルについて紹介します。
目次
背景・課題
ZOZOTOWNで商品を注文すると、注文した商品に応じて様々な大きさの箱や袋(以下ではまとめて梱包資材と呼びます)で商品が届きます。注文した商品が全部入ればどの梱包資材でも配送はできますが、環境や物流リソースの観点からできるだけ小さい梱包資材を選びたいです。
注文された商品が1つだけであれば、その商品が入る最小の梱包資材を選ぶことは簡単ですが、複数の商品が同時に注文された場合には、全ての商品を梱包できる最小の資材を選ぶことはなかなか難しい問題です。
大き過ぎず小さ過ぎない最適な梱包資材を選ぶことで、配送費用や梱包資材の無駄が減少し、箱内の隙間が減ることで緩衝材の量や梱包品質も改善することが期待できます。また昨今問題となっている物流リソースの不足にも貢献できる非常に重要な課題です。

梱包資材を選ぶアルゴリズム
最小の梱包資材は以下の方法で選ぶことができます。
- 候補となる梱包資材を小さい順に並べ、順に以下を試す。
- 注文商品全てをはみ出すことなく梱包可能であればその資材を採用する。梱包できない場合は次の候補に移る。
ここで問題となるのが、候補となる梱包資材に注文商品が梱包可能なのかどうかを判定することです。これは、典型的な組合せ最適化問題1である(3次元)直方体詰込み問題を解くことで判定できます。
直方体詰込み問題とは
(3次元)直方体詰込み問題は大きな直方体の容器に複数の大きさの異なる直方体(アイテム)を詰込む方法を考える問題の総称です。下記のようなバリエーションの問題が研究されています。
- アイテムをなるべく少ない数の容器に詰込む3次元ビンパッキング問題
- 1辺の長さが可変な容器を仮定して、アイテムをなるべく小さい容器に詰込む3次元ストリップパッキング問題
今回解きたいのは容器を梱包資材、アイテムを注文商品として、梱包可否を判別する問題です。厳密には最適化問題ではありませんが、上記のバリエーションに容器の数や大きさを固定する制約条件を追加し、目的関数を削除した(定数として扱うことと同じ)最適化問題の一種として扱うことができます。
直方体詰込み問題の解法
直方体詰込み問題はNP困難な組合せ最適化問題の中でも計算コストが高い問題として知られています。例えば物流コンテナにダンボールを詰込む問題などアイテム数が数十〜数百規模になると、実用的な時間で厳密な最適解を求めることが難しく、ヒューリスティックな方法を採用することが多いです。
一方で、今回扱うのは注文商品を梱包資材に詰込む問題です。1度に注文される商品は10点以下であることがほとんどであるため、問題を定式化して最適化ソルバーで解くアプローチも現実的です。ZOZOの梱包資材の選択では最適化ソルバーに加えて、ルールベースやヒューリスティックなども含めた複合的なアルゴリズムをとっていますが、本記事では最適化ソルバーを利用した方法について紹介します。
問題の定式化
直方体詰込み問題を最適化ソルバーで解くために、直方体詰込み問題を混合整数最適化問題として定式化します。
OR学会機関誌の記事に2次元ストリップパッキングの定式化とプログラムがあるので、それを参考に3次元の詰込み可否判定問題を定式化します。
https://orsj.org/wp-content/corsj/or63-12/or63_12_762.pdforsj.org
前提として、使用する梱包資材や梱包する商品は全て直方体としてみなすことができて、3辺の長さがあらかじめわかっているとします。
回転や折りたたみを許さないモデル
まずは簡単のためにアイテムの回転や折りたたみは考慮しないモデルを考えます。
定数
,
,
: 梱包資材の3辺の長さ。
,
,
: アイテム
の3辺の長さ。
決定変数
,
,
: アイテム
の位置座標。
,
,
: アイテム
がアイテム
より各軸方向で原点側にある時1、そうでない時0をとる変数。
目的関数
前述の通りなし(定数)。
制約条件
全てのアイテムが梱包資材内に収まる制約
2つのアイテムが各軸の方向で重ならない制約
となるアイテム
について制約がかかります。各制約はそれぞれ
,
,
が1を取る時だけ有効になります。
また、2つのアイテムが3軸の前後関係の中でどれか1つは重ならない必要があるので、次の制約も必要です。
商品の回転や折りたたみを許さない場合は、以上の制約で梱包可否を判定するモデルとしての定式化は完了です。
回転と折りたたみを許すモデル
商品は梱包資材に対して様々な向きに回転して詰め込むことができます。また、Tシャツなど一部のカテゴリの商品は、標準の梱包状態からさらに2つ折りにして梱包することもできます。
回転や折りたたみといった形状変化はアイテムの寸法の変化として考えることができます。上記の定式化を以下のように変更することで寸法変化に対応できます。
追加の定数
,
,
: アイテム
が形状
を採用する時の3辺の寸法。
決定変数の変更
: アイテム
が形状
を取る時1、それ以外で0をとる変数を追加。
- 定数としていた
,
,
を以下の式に変更する。
追加の制約条件
: アイテム
はどれか1つの形状を採用するという制約
荷姿を整えるための目的関数
梱包資材とアイテムの寸法を用意して、上記の最適化モデルを最適化ソルバーに入力すると、モデルの実行可能性で梱包可否の判断が可能です。梱包可能な入力データを作成し、解いた結果を図示すると次のようになります。
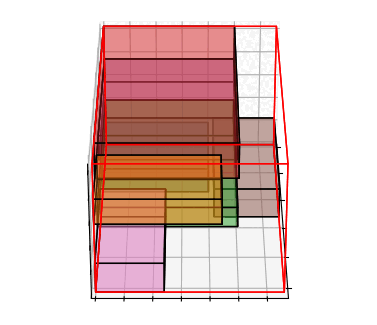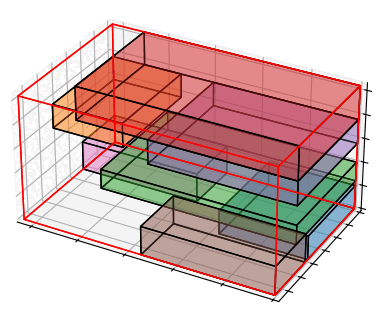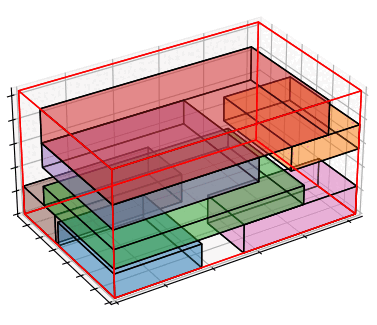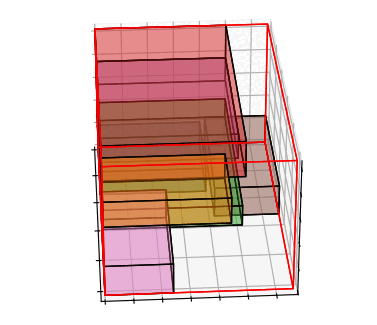
目的関数が無いモデルは梱包可否の判定のためには十分ですが、計算結果を見るとアイテムが宙に浮いているなど現実的ではない荷姿が出てくることがあります。
荷姿の情報も参考情報として提示したい場合は、荷姿に関する目的関数を追加することで比較的現実的な計算結果が得られます。全商品の密度が同じだと仮定して、Z軸方向の重心位置を最小化する目的関数を設定すると次のような計算結果が得られます。

ソルバーが扱える目的関数には制限がありますが、シンプルな目的関数でもやや現実的な荷姿を得ることができました。
まとめ
本記事では梱包資材を選択するための数理最適化モデルについて紹介しました。
ZOZO NEXTでは、一緒に業務改善を見据えた研究開発をしてくれる方を募集中です。ご興味のある方は、以下のリンクからぜひご応募ください。