混合整数最適化でスケジューリング問題を扱うテクニック 〜カスタマーサポートのWFMを例に〜

数理最適化

header

はじめに

こんにちは。ZOZO Researchの千代です。

ZOZO Researchでは類似アイテム検索やおすすめアイテムのレコメンドといった機能開発の他に、様々な技術を用いたバックエンド業務の効率化にも取り組んでいます。

ZOZOTOWNのカスタマーサポートで実施しているワークフォースマネジメント（以下WFM）もその1つです。WFMで必要となるタスク割当て問題を数理最適化問題の一種である混合整数最適化問題として定式化し、最適なタスク割当てを計算しています。

この記事では、カスタマーサポートのWFMでの利用を例に、混合整数最適化でスケジューリング問題を定式化するテクニックについて説明します。

目次

ワークフォースマネジメントとは

ワークフォースマネジメントとは、人的資源を適切に配置し、より効率的で高いパフォーマンスを発揮することを目指す取り組み全般を表す言葉です。

ZOZOTOWNのカスタマーサポートでは、サービスレベル向上のためのWFMの一環として、時間帯別の問い合わせ数の予測に基づいてスタッフのタスク割当てを求めるスケジューリング問題を解いています。

例えば朝は電話1による問い合わせが多いので、電話の対応に当たるスタッフを増やす、といった対応を計算により実施しています。

スケジューリング問題とは

スケジューリング問題とは、人や機械といったリソースに対して仕事などのスケジュールを割当てる問題を指す言葉で、具体的な問題としてはシフトスケジューリング問題やジョブショップ・スケジューリング問題などが挙げられます。

この記事では以下のような問題を想定して説明していますが、使っているテクニックはスケジューリング問題全般で利用可能なものです。説明用の簡略化したモデルになっているため、実務で使っているモデルとは詳細が異なります。

この記事の問題設定

  • 各スタッフの1日の時間帯ごとのタスクの割当てを考える問題です。
  • タスクとは各種チャネルの問い合わせへの対応やその他の個人タスク、休憩のいずれかを表します。
  • 時間は15分のタイムスロットに区切って考えます。
  • 以下のデータは入力として与えられるとします。
    • その日の出勤者および出勤時間帯（早番、遅番など）
    • 各時間帯、各チャネルの問い合わせ数予測
    • 各スタッフの実施可能なタスク
    • 問い合わせ対応のタスクについては、各スタッフのタスクに対する処理能力

タスク割当て例

スケジューリング問題を解くためのアプローチ

スケジューリング問題は多くの場合NP困難となるので、従来は、

  • 重み付き制約充足問題として定式化し、CPソルバーを使って解く方法
  • タブーサーチなどメタヒューリスティクスアルゴリズムを使って解を求める方法

といった近似解法を用いたアプローチが一般的でした。しかし近年アルゴリズムやハードウェアの進歩により、「混合整数最適化問題として定式化し、厳密最適解やそれに準ずる解を求める方法」も選択肢として一般的になってきました。

本記事でも、混合整数最適化問題として扱うアプローチを紹介します。

数理最適化問題とは

今回使用する混合整数最適化問題は、数理最適化問題の1つのカテゴリです。混合整数最適化問題について説明する前に、まず数理最適化問題について簡単に紹介します。

数理最適化問題とは、条件を満たす候補の中から目的に対して最適なものを数学的に見つける問題です。数理最適化問題は次の3つの要素でできています。

  • 決定変数：意思決定や制御の対象で、値を決めたいもの
  • 目的関数：決定変数が目的に対して良いか悪いかを判断するための関数
  • 制約条件：候補となる決定変数が満たす必要のある条件

制約条件を満たした上で、目的関数を最小化または最大化する決定変数を見つける問題が数理最適化問題です。

混合整数最適化問題とは

混合整数最適化問題とは数理最適化問題の中で、整数値を取る変数を含むもので、英語ではMixed Integer Programming (MIP)やMixed Integer Optimization (MIO)と呼ばれています。

整数変数を使うことで、割当てや順序のような組合せ的な問題が表現できるようになります。

今回は、混合整数最適化問題のなかでも目的関数と制約式に線形のものだけを含んだ、混合整数線形最適化問題のみを扱います。最近では線形でない制約式や目的関数の問題も解けるようになってきていますが、まだまだ解ける問題の規模は限定的で、混合整数最適化問題といえば多くの場合は混合整数線形最適化問題を指すのが一般的です。

混合整数（線形）最適化問題は例えばPythonのpulpというモデリングライブラリを使うと簡単に実装できます。問題を解くためには最適化ソルバーというソフトウェアが必要ですが、pulpをインストールするとCbcというOSSの最適化ソルバーが一緒にインストールされるため、そのまま計算を実行できます。

github.com projects.coin-or.org

混合整数最適化問題でスケジューリング問題を扱うテクニック

ここからはWFMでのタスク割当て問題を例に、スケジューリング問題を混合整数最適化問題として定式化する際のテクニックをいくつか紹介していきます。

数式を使って説明していきますが、前述の通り変数の一次式しか登場しないので意味するところがわかれば非常に簡単です。また説明の簡潔さのため、一部厳密性を欠いた表現をしている箇所があります。ご了承ください。

以下では最適化問題の決定変数は小文字で、入力として与える定数は大文字で表すこととします。

準備

まず準備として、タスクの割当てを表現する変数を以下のように用意します。

  • x_t^{sj}\in\{0,1\}: スタッフ sが時刻 tにタスク jを行う時1、それ以外で0をとる0-1整数変数

各スタッフは勤務時間中には同時に1つのタスクを実行し、出勤前や退勤後はタスクを何も実行できません。これは以下のような制約式で表現できます。ただし、前述の通り休憩時間も1つのタスクとして扱っています。

  • \sum_{j} x_t^{sj}=1（ tが sの勤務時間内の場合）
  • \sum_{j} x_t^{sj}=0（ tが sの勤務時間外の場合）

この変数 x_t^{sj}を使って各種制約を表現していきます。

処理能力に関する制約

問い合わせ数の予測に対して、すべての問い合わせをまかなう制約を考えます。これはある時刻に稼働している全スタッフの、その問い合わせに対応するタスクの処理能力の合計が、予測された問い合わせ数を上回っているという制約で表現できます。

スタッフ sのタスク jについての処理能力を P_{sj}、時刻 tのタスク jの業務量の予測を D_{t}^{j} とすると、次のような式になります。

  • \sum_{s} P_{sj}x_t^{sj} \geq D_{t}^{j}（全ての t, jについて）

この制約式は、全ての時間帯で必ずリソースが問い合わせ予測を上回ることを求めています。しかし現実的には、問い合わせ量の瞬間的な増大などあらゆる事態に対応できるようなリソースを常に確保しておくことは困難です。

上記の制約式のままでは全ての時間帯、問い合わせチャネルで予測量を上回るリソースを用意していなければ最適化問題が実行不可能となり、モデルとして使い勝手がよくありません。そのためこの制約を変更します。新しく0以上の実数値を取る変数として、

  • v_{t}^{j} \in \mathbb{R}_{\geq 0}: 時刻 tにタスク jで不足する処理能力を表すペナルティ変数

を用意します。この変数を使って上の制約を以下のように変更します。

  • \sum_{s} P_{sj}x_t^{sj}+v_t^j\geq D_t^j（全ての t, jについて）

また制約式の変更だけでなく、ペナルティ変数の総和2を最小化するように目的関数を変更します。これによりもし全ての問い合わせに対応できない状況であっても、対応できない問い合わせの量を最小化する問題として計算でき、常に解が得られるようになります。

常に解が得られることで、例えば対応できない問い合わせの数が多すぎる時に、事前にリソースの調整をするといった対応を行えます。

タスクの最低継続時間

実際のオペレーションでは、割当てられたタスクが頻繁に変わるような運用は好ましくありません。そのため、各タスクを開始したら最低45分間は同じタスクを継続するといった制約を追加したい場合があります。このようなタスクの最低継続時間制約を実現する方法を紹介します。

タスク開始変数の導入

スタッフのタスクの継続時間をはかるために、次のような変数を新たに追加します。

  • y_t^{sj}\in \{0, 1\}: スタッフ sが時刻 tにタスク jを開始したら1、そうでない時0

変数 y_t^{sj}と x_t^{sj}の関係は、一例を挙げると以下の図のようになります。

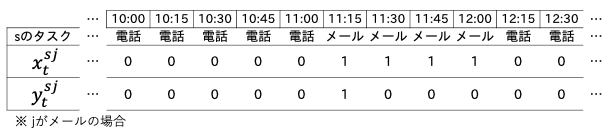
タスク割当て例

図のように、 y_t^{sj}は x_{t-1}^{sj}が0で、 x_{t}^{sj}が1のときだけ1をとり、他は0をとる変数です。この関係は以下のような制約を追加することで表現できます。

  • 制約1: x_t^{sj}-x_{t-1}^{sj}\leq y_t^{sj} 3
  • 制約2: y_t^{sj}\leq x_t^{sj}
  • 制約3: y_t^{sj}\leq 1-x_{t-1}^{sj}

この制約によって表される y_t^{sj}の値の候補を書き出すと次の表のようになり、タスク開始変数が表現できていることがわかります。

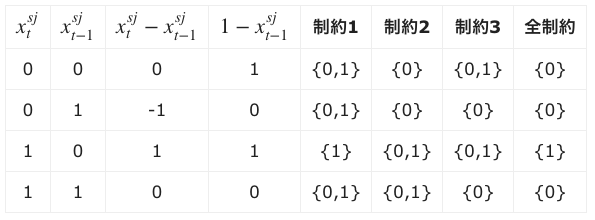
変数yの候補

最低継続時間制約の表現

前節で定義したタスク開始変数を用いれば、タスクの最低継続時間の制約を簡単に表現できます。例えば一度タスクを開始したら最低3スロット以上継続するという制約を表したい場合は次のようになります。

  • y_t^{sj}\leq x_\tau^{sj}, \forall \tau \in \{t,t+1,t+2\}

またこのテクニックを応用することで、例えば「1回目の休憩と2回目の休憩の間は2時間以上の間隔をあける」といった制約も表現できます。

複数の目的関数への対応

WFMのタスク割当てモデルでは、処理能力不足のペナルティを最小化することを目的関数としていました。しかし新型コロナウイルス感染症の影響で、休憩室が密になることを回避するために、同時に休憩を取る人数をできるだけ少なくしたいという要望がでてきました。

同時に休憩を取る人数をできるだけ少なくするという問題は、同時に休憩を取る人数の1日の中での最大値を最小化する問題として表現できます。

多目的最適化

「処理能力不足のペナルティ最小化」と「同時休憩人数最小化」のような複数の目的関数を持った最適化問題は多目的最適化問題と呼ばれています。

多目的最適化問題に対する対処としては、重みをかけて足し合わせ1つの目的関数にする方法がシンプルで一般的ですが、今回のように単位の全く異なる値同士の時は重みのパラメータを決めるのがなかなか難しいです。

ここでは別の方法として2段階最適化というものを紹介します。

2段階最適化

2段階最適化は、優先順位の明確な2つの目的関数について、段階的に最適化問題を解いて最適解を求める方法です。タスク割当ての例で、「同時休憩人数最小化」が第1優先、「処理能力不足のペナルティ」が第2優先という設定を仮定して方法を説明します。

  1. 「同時休憩人数最小化」のために、同時休憩人数の最大値を最小化する問題として最適化問題を解きます。この時「処理能力不足のペナルティ最小化」については考慮しません。
  2. 1.で求められた最適値（最小な同時休憩人数の最大値）を使って、同時休憩人数がその値以下になるという制約を追加し、「処理能力不足のペナルティ最小化」を目的関数として再度最適化問題を解きます。

この順番で問題を解くことによって、同時に休憩を取る人数を最小にした上で、処理能力不足のペナルティを極力小さくできます。

まとめ

この記事ではカスタマーサポートでのタスク割当問題を例に、混合整数最適化問題でスケジューリング問題を扱うときのテクニックとして、

  • 処理能力不足のペナルティ最小化
  • タスク最低継続時間制約
  • 2段階最適化

を紹介しました。

混合整数最適化問題は不等式制約や整数変数をうまく使うことで、様々な種類の問題を定式化することが可能です。

おわりに

ZOZOテクノロジーズでは技術の力で事業に貢献してくれる仲間を募集中です。ご興味のある方は、以下のリンクからぜひご応募ください！

tech.zozo.com

  1. 新型コロナウイルス感染症の影響で、ZOZOTOWNカスタマーサポートの電話窓口は現在受付停止しています。↩

  2. ペナルティという値の性質上2乗和をとりたくなる時がしばしばありますが、混合整数線形最適化では2乗和は扱えません。区分線形関数を使うと線形モデルのままで近似できますが、変数の数が増えモデルは複雑になります。↩

  3. 目的関数や他の制約次第では制約1だけで表現できる場合もあります。例えばタスクの切り替え回数（タスク開始変数の和）の最小化など、 y_t^{sj}を最小化するような項が目的関数に入っているときは、制約1だけで十分です。↩

カテゴリー