ZOZO研究所でインターンをしている松井です。本記事では、cross-domain画像検索とdeep metric learningの概要と、cross-domain画像検索で良い精度を達成するためのテクニックを取り上げます。
metric learningの概要
metric learningとは、データ間の関係を表す計量（距離や類似度など）を学習する手法です。 画像分類や、画像検索などに応用できます。 意味の近いデータの特徴量どうしは近く、意味の異なるデータの特徴量どうしは遠くなるような計量を学習 します。 意味の近いデータのペアを positive pair 、意味の異なるデータのペアを negative pair と呼びます。
deep learningが出てくる前の代表的な手法として、マハラノビス距離の共分散行列を学習させる手法があります。
：データの特徴量
：パラメータ（共分散行列）
このを、positive pairならば小さく、negative pairならば大きくする損失関数で学習をします。
前述したマハラノビス距離の式においてと分解すると、以下のように表すこともできます。
：ユークリッド距離
つまり、マハラノビス距離の共分散行列を学習することは、ユークリッド距離においてpositive pairならば近く、negative pairならば遠くなるような特徴量を抽出する行列
を学習することとも捉えられます。
をかけることは線形写像ですが、その代わりに非線形写像をdeep learningで学習する手法が、deep metric learning です（以下、DMLと略します）。
：非線形写像
：パラメータ
metric learningの応用
metric learningの代表的な応用である、 fine-grained image classification と cross-domain画像検索 を紹介します。
fine-granined image classification
fine-grained image classification とは、以下の入出力を持つタスクです。
- 入力：画像
- 出力：画像に映る物体のクラス
fine-grained image classificationでは車や鳥といった大雑把なクラスを予測するのではなく、 車種や鳥の種類など、より細かいクラス を予測します。 クラス数が多く、クラスあたりの画像数が少ない 状況です。
metric learningを用いて解くとき、positive pairとnegative pairを以下のように定義します。
- positive pair：同じクラスの画像ペア
- negative pair：異なるクラスの画像ペア
そして、学習した距離を用いたk-nearest neighborで分類問題を解きます。 つまり、分類したいデータに最も近いk個のデータのクラスを見て分類します。
metric learningでは、学習時の入力が画像1枚ではなく画像のペアなので、1クラスあたりの学習データを大幅に増やすことができます。 そのため、クラスあたりの画像数が少ないfine-grained image classificationにmetric learningは適しています。
また、手法の評価方法は予測クラスが合っていれば正解として、accuracyを用いることが多いです。
cross-domain画像検索
cross-domain画像検索とは、以下の入出力を持つタスクです。
- 入力：クエリ画像
- 出力：クエリ画像に対応する、ドメインの異なる画像
今回は、ファッションの画像を扱います。入出力は具体的に以下になります。
- 入力：スナップ写真中の検索したいアイテム領域（以下street queryとする）
- 出力：そのアイテムの商品画像（以下shop imageとする）
metric learningを用いて解くとき、positive pairとnegative pairを以下のように定義します。
- positive pair：同じ商品のstreet queryとshop imageのペア
- negative pair：異なる商品のstreet queryとshop imageのペア
商品IDをクラスとみなすと、クラスあたりの画像が少ない状況はfine-grained image classificationと同じです。 ですから、同様の理由でcross-domain画像検索にもmetric learningを用いることができます。
fine-grained image classificationと異なる点は以下の3が挙げられます。
- ペア間で画像のドメインが異なる
- クラス（商品ID）あたりの画像数が1枚だけで、より少ない
- 同じ商品なのに似ていないペア（hard positive pair）や、異なる商品なのに似ているペア（hard negative）がいくつか存在する
手法の評価方法は、検索結果の上位k個にstreet queryと同じ商品が含まれていれば正解として、top-k accuracyを用いることが多いです。
metric learningの研究では、モデルの評価は主にfine-grained image classificationのタスクで行われています。 cross-domain画像検索を用いた評価は、主流ではありません。
DMLの手法を構成する項目
DMLの手法はいくつかの項目で構成されます。 例えば、計量として類似度と距離どちらを用いるのかや、どのような損失関数で距離を小さく・大きくするかなどがあります。
この章では以下の4つの各項目において、どのような選択肢があるのかを紹介します。
- サンプリング
- ネットワークの構造
- 計量
- 損失関数
サンプリング
metric learningの文脈におけるサンプリング方法とは、入力データの作り方です。 代表的なものとして、contrastive sampling、triplet samplingがあります。
contrastive samplingのバッチ内のサンプルは以下になります。
：positive pair
：negative pair
：pairの起点となるサンプル（以下、anchorとする）
- 例：street query
：anchorに対して、positiveな関係にあるサンプル（以下、positiveとする）
- 例：同じ商品のshop image
：anchorに対して、negativeな関係にあるサンプル（以下、negativeとする）
- 例：異なる商品のshop image
triplet samplingのバッチ内のサンプルは以下になります。
$$ (a, p, n) $$
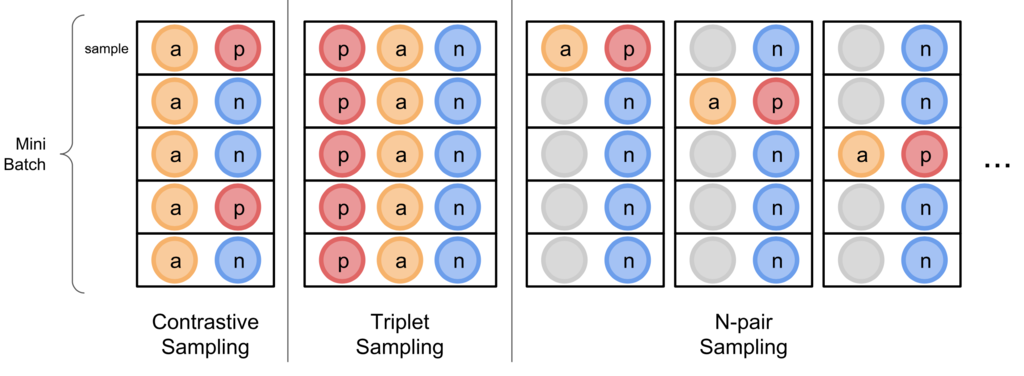
また、N-pair samplingが以下の論文で提案されました。
(K. Sohn. 2016) Improved Deep Metric Learning with Multi-class N-pair Loss Objective.
N-pair samplingのバッチ内のサンプルは以下になります。
$$ (a_i, p_i, \left\{n_j\right\}_{j=1, j \neq i}^B) $$
：anchorとpositiveの添字
：バッチサイズ
バッチ内の他の商品のpositiveをすべてnegativeとして扱います。 contrastive samplingやtriplet samplingに比べ、1サンプルにつき複数のnegativeを考慮できます。
metric learningでは、学習が進むに連れて、十分離れたnegativeが増えてきます。 1サンプルにつき1つのnegativeしか考慮しないと、十分離れたnegativeをサンプルしてしまった場合、重みが更新されません。 そのため、contrastiveやtripletよりN-pairのほうが学習の効率が良いとされています。
ネットワークの構造
基本的な構造は、ImageNetでpre-trainしたCNNの先にFC（全結合）層を1層つけた形になります。
構造の項目として、今回は以下を考えました。
- CNNをstreetとshopで分けるか
- FCをstreetとshopで分けるか
上の2つの項目はcross-domain画像検索のときのみ考えます。 理由は、ドメインごとに異なる特徴抽出器を学習させたほうが精度を上げられる可能性があるためです。
計量
代表的な計量として以下の3つが挙げられます。
- 類似度
- コサイン類似度
- 内積
- 距離
- ユークリッド距離
※正しくは、類似度を計量と呼びません。距離と類似度の総称が無いため、この記事では便宜上、まとめて計量と呼ぶことにします。
損失関数
この記事では、効率の良いN-pair samplingについてのみ扱っていくので、N-pair samplingのときの損失関数について取り上げます。 今回は、以下の2つの損失関数を取り上げます。
- hinge loss
- SCE（softmax cross-entropy）loss
hinge loss
hinge lossは以下の式で表されます。
$$ L_{U} = \frac{1}{B} ( \sum_{i=1}^B{ \sum_{j=1 , j \neq i}^B{ \max( 0, d_p^{(i)} - d_n^{(i,j)} + m ) } }) $$
$$ d_p^{(i)} = d(x_{U}^{(i)}, x_{V}^{(i)}) $$
$$ d_n^{(i, j)} = d(x_{U}^{(i)}, x_{V}^{(j)}) $$
：マージン
：negativeの添字
：positive pair間のユークリッド距離
：negative pair間のユークリッド距離
：ドメイン
hinge lossは、を
より小さくしようし、
という式を満たすよう学習させます。
以下の図のように、positiveとの距離+マージンの外にnegativeを追いやるよう学習させます。
なお、計量が類似度ならば符号を逆にします。
また、上の式はドメインの画像特徴量をanchorとしていますが、
と
を入れ替えた
との和を最終的な損失関数とします。
$$ L = L_{U} + L_{V} $$
SCE loss
SCE lossは以下の式で表されます。
$$ L = - \frac{1}{B} \sum_{i=1}^B \sum_{k=1}^B y_{(i,k)} \log{ P_i(k) } $$
確率を1に、それ以外の確率は0にしたい場合、
の項だけが残るよう、
を以下のように定義します。
$$ y_{(i,k)} = \begin{cases} 1 & (k=k_1) \\ 0 & (k \neq k_1) \end{cases} $$
類似度を用いて確率を表すとSCE lossは以下のように表せます。
$$ L = - \frac{1}{B} \sum_{i=1}^B \sum_{k=1}^B y_{(i,k)} \log{ \frac{ \exp{s^{(i,k)}} }{ \sum_{j=1}^B \exp{s^{(i,j)}} } } $$
：サンプル
今、positive pairの類似度を大きくし、negative pairの類似度
は小さくしたいです。
すなわち、
にして、それ以外の確率は0にしたいので、
の項だけ残します。
$$ L = - \frac{1}{B} \sum_{i=1}^B \log{ \frac{ \exp{s^{(i,i)}} }{ \sum_{j=1}^B \exp{s^{(i,j)}} } } $$
$$ = \frac{1}{B} \sum_{i=1}^B \left\{ - s^{(i,i)} + \log{ \sum_{j=1}^B \exp{s^{(i,j)}} } \right\} $$
上の式は、類似度を使ったhinge lossと似ています。
ただ、negative sample ついてhinge lossでは平均をとっていますが、SCE lossではLogSumExpをとっています。
hinge lossではバッチ内のnegative pairが離れていくに連れlossが小さくなります。
しかし、 SCEではバッチ内に1つでも十分離れていないnegativeが存在すればlossは大きいまま です。
よって、以下の論文ではSCE lossのときの学習効率のほうが良いとされています。
(K. Sohn. 2016) Improved Deep Metric Learning with Multi-class N-pair Loss Objective.
fine-grained image classificationで有効な慣習がcross-domain画像検索では有効とは限らない
今回、cross-domain画像検索を試作しました。 そのとき、fine-grained image classificationでは有効である慣習の1つが、cross-domain画像検索では有効でないことがわかりました。
試作の条件
以下の条件で試作を作りました。
- サンプリング：N-pair sampling
- ネットワークの構造：CNN, FC共有
- 計量：コサイン類似度
- 損失関数：hinge loss
- マージン：1.0
CNNはInception V3を用い、ImageNetでpre-trainした重みを採用しました。 CNNを、出力が2048次元の特徴抽出器としました。 CNNの重みはmetric learningでfine-tuningしました。
FCの出力は512次元にしました。
データセットの各サンプルは以下の形をしています。
$$ (I_{strt}, I_{shop}) $$
：WEARのスナップ画像からSSDで検出したアイテム領域
：それに対応するZOZOの商品画像
trainデータでは60,000サンプルを使用しました。
最適化手法はAdamを用いました。Adamのハイパーパラメータはとしました。
バッチサイズは30としました。
1,000 iteration学習させました。
評価方法
評価指標は Acc.@k/N（Top-k Accuracy against N items） を用いました。
学習したネットワークで抽出したstreet queryとshop imageの特徴量でk近傍探索を行います。 つまり、N枚のshop imageから、あるstreet queryと似ている画像を検索します。 そして、検索結果の上位k個の中に同じ商品のshop imageが含まれれば正解=1とします。 含まれなければ、不正解=0とします。 N枚のstreet queryに対し、上記の操作を繰り返し、平均を取った値がAcc.@k/Nです。 値が高いほど、良いです。
通常、Nの方は明記されませんが、以下の論文ではNが大きくなるに連れてAcc.@kの値は減少する結果が出ています。 ですから、結果の比較をしやすくするため、あえてNを明記しました。
今回は、Acc.@20/1000を用いました。 以降、簡単のため、この指標を単に精度と呼ぶことにします。
評価に用いるtestデータはtrainデータとは異なる1,000サンプルを用いました。
結果
- HingeCosM1.0：試作
- ImageNet：ImageNetで学習したCNNにより抽出した特徴量を用いた方法
試作は、ImageNetよりも精度が低かったです。
精度改善のため、hinge lossがちゃんと機能しているかを調べました。 バッチ内のanchor・positive・negative間のコサイン類似度が学習によってどう変化するかをプロットしました。
- anc_pos：positive pair間のコサイン類似度の平均
- anc_neg：negative pair間のコサイン類似度の平均
- pos_neg_strt：street query間のコサイン類似度の平均
- pos_neg_shop：shop image間のコサイン類似度の平均
学習が進むにつれ、anc_posとその他との差が開いていったことがわかります。 すなわち、同じ商品は近くに、異なる商品は遠くに埋め込まれたと考えられます。 この図だけ見ると、hinge lossは意図した通りに機能していたようです。
ここで、学習による精度の変化も見てみます。
初めは、一気に精度が上がり、そこから徐々に落ちていったことがわかります。
また、検索結果も見てみます。
query item
正解のshop image
ImageNet
HingeCosM1.0
各手法の検索結果の上位20個のshop image（左から右、上から下の順）
ImageNetの結果ほうがstreet queryに近い柄のアイテムが検索されました。
次に、testデータの、各shop queryに対する1,000 shop imagesのコサイン類似度のヒストグラムを見ました。
横軸がコサイン類似度で、縦軸は頻度です。 類似度が1か-0.3付近に集中していることがわかります。 つまり、どちらかといえば似ているshop imageの類似度はほぼ1になっていると考えられます。 この現象の原因は、学習データにhard positive pair（同じ商品だが似ていないペア）が多く含まれるためだと考えられます。 hard positive pairの類似度を上げようとすると、学習していないnegative pairのうち、hard positive pairより似ているものの類似度はより高くなる可能性があります。 つまり、同じ商品なのに似ていないペアの類似度を上げようとすると、より似ている異なる商品との類似度も上げてしまう可能性があるということです。 そのため、あまり似ていない商品が含まれる結果になったと考えられます。 すなわち、マージン=1.0だと、hard positive pairに引っ張られて過学習を起こしやすいと考えられます。 そこでマージンを小さくすることで、どちらかといえば似ている商品の類似度を程よい値（0.5など）にでき、精度があがると考えました。
実験
マージンを小さくすると精度があがるかを検証するための実験を行いました。 比較する条件は以下の3つです。
- HingeCosM1.0：マージン=1.0（先程の試作）
- HingeCosM0.5：マージン=0.5
- HingeCosM0.1：マージン=0.1
結果
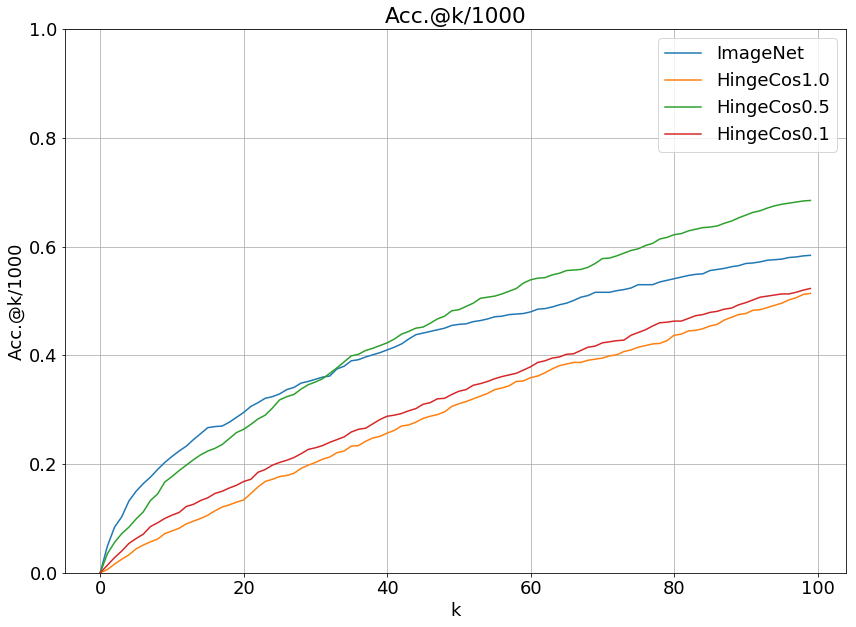
マージン=0.5のときが最も良い精度となりました。
query item
正解のshop image
ImageNet
HingeCosM1.0
HingeCosM0.5
HingeCosM0.1
各手法の検索結果の上位20個のshop image（左から右、上から下の順）
検索結果も、マージン=0.5のときの柄が最もshop queryに似ていました。 なお、shop queryの色と検索結果のshop imageの 色が異なるのは、同じ商品でも異なる色のペアがデータセットに含まれていたため だと考えられます。 そのようなペアをデータセットから除けば、検索結果に色も反映できる と思われます。
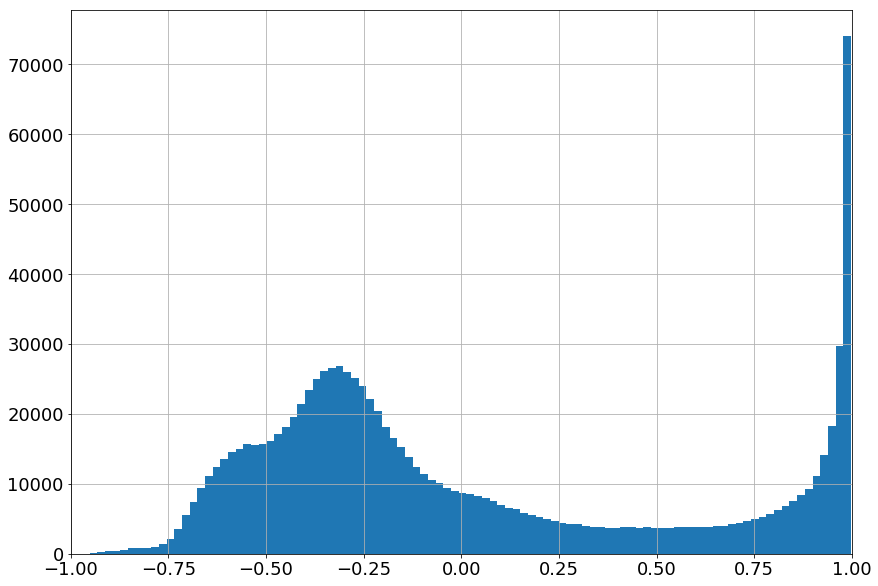
次に、testデータのコサイン類似度のヒストグラムも見てみます。
HingeCosM1.0
HingeCosM0.5
HingeCosM0.1
マージン=1.0にくらべ、マージン=0.5のときの類似度は-0.25から1にかけてなだらかに分布してるのがわかります。 マージン=0.1のときはそもそも類似度の差が開いていないため、精度が悪かったと考えられます。
結論
既存のmetric learningの研究では、マージンは大きいほうが良いという慣習がありました。 しかし、既存の研究では、fine-grained image classificationで評価することがほとんどです。
今回、マージンの大きさによるcross-domain画像検索の精度を計測したことで、cross-domain画像検索においてマージンを大きくすることは有効でないことがわかりました。 マージンを大きくするとhard positiveに引っ張られてしまい、hard positiveが多く含まれるcross-domain画像検索では精度が落ちることがわかりました。
また、マージン以外にも、既存の研究で有効とされている慣習がcross-domain画像検索では有効とは限らない可能性があると考えられます。
Cross-domain画像検索で有効なテクニックの探索
さらなる改善のため、マージン以外の項目も同時に探索しました。
探索範囲
以下の項目の組合せを探索しました。
- CNNの構造
- 共有するか
- 分けるか
- CNNの重み
- ImageNetの重みで固定するか
- fine-tuingするか
- FCの構造
- 共有するか
- 分けるか
- 計量
- 類似度
- コサイン類似度
- 内積
- 距離
- ユークリッド距離
- 類似度
- 損失関数
- hinge loss
- SCE loss（計量が類似度のときのみ）
- マージン（hinge lossのときのみ）
- 1.0, 0.7, 0.5, 0.3, 0.1（計量がコサイン類似度のとき）
- 625, 437, 312, 187, 62（計量が内積のとき）
- 12250, 3240, 1440, 490, 40（計量がユークリッド距離のとき）
FCを分ける場合、重みの初期値を共有にしないと精度が一向に上がりませんでした。 初期値を共有にすることで学習が安定したので、今回はFCを分けるとき、初期値は共有しました。
ユークリッド距離とSCE lossを同時に用いるなどの妥当でない組合せを除き、230条件を探索しました。
1000 iterationだけ学習させ、10 iterationごとに精度を見て3回連続で落ちた場合、学習を打ち切りました。 評価には最後のiterationの重みを用いました。
上記の条件以外は、試作の条件と同じです。
マージンの探索範囲は、コサイン類似度のときのマージンの範囲を各計量に応じて変換しました。 学習初期の画像特徴量ベクトルのノルムが約25だったので以下の式で変換しました。
内積のときは以下の変換を用いました。
$$ m_{dot} := ||x||^2m_{cos} = 625 m_{cos} $$
：内積のときのマージン
：画像特徴量ベクトルのノルム
：コサイン類似度のときのマージン
内積は、コサイン類似度に両ベクトルのノルム（）をかけたものなので、マージンも
倍しました。
ユークリッド距離のときは以下の変換を用いました。
$$ m_{euc} := \sqrt{ 2 (1-\sqrt{1-m_{cos}^2}) }||x|| $$ $$ = 25\sqrt{ 2 (1-\sqrt{1-m_{cos}^2}) } $$
：ユークリッド距離のときのマージン
また、実装の都合上、距離ではなく距離の二乗を採用したため、マージンも二乗したを用いました。
ユークリッド距離のときのマージンの変換の導出は、付録1で説明します。
結果
探索範囲の内、最良の条件は以下で、Acc.@20/1000=48.4％に達しました。
- CNNの構造：共有する
- CNNの重み：fine-tuingする
- FCの構造：分ける
- 計量：内積
- 損失関数：hinge loss
- マージン：187
なお、349 iterationで打ち切られていたため1000 iterationまで学習させたところ、Acc.@20/1000=57.1％に達しました。
以降、上の条件をHingeDotM187SpFcと呼ぶことにします。
下の図からわかるように、前の章で最も良かったHingeCosM0.5に比べて大幅に精度が良くなりました。
検索結果は以下になります。
query item
正解のshop image
HingeCosM0.5
HingeDotM187SpFc
各手法の検索結果の上位20個のshop image（左から右、上から下の順）
HingeDotM187SpFcの方が、street queryの柄により近い結果となりました。
また、各項目による精度の違いを見ていきます。
下記の表では計量とCNNの重みの条件以外は、CNNとFCともに共有、Hinge lossで固定したときの精度です。
| 条件 | 計量 | CNNの重み | Acc.@20/1000 |
|---|---|---|---|
| HingeCosM0.5 | コサイン類似度 | fine-tuning | 0.283 |
| HingeCosM0.5Fx | コサイン類似度 | 固定 | 0.152 |
| 条件 | 計量 | CNNの重み | Acc.@20/1000 |
|---|---|---|---|
| HingeDotM187 | 内積 | fine-tuning | 0.469 |
| HingeDotM187Fx | 内積 | 固定 | 0.132 |
| 条件 | 計量 | CNNの重み | Acc.@20/1000 |
|---|---|---|---|
| HingeEucM324 | ユークリッド距離 | fine-tuning | 0.442 |
| HingeEucM324Fx | ユークリッド距離 | 固定 | 0.136 |
Mの後の数字はマージンです。 どの計量においてもCNNをfine-tuningしたほうが良かったです。 また、計量に関して内積とユークリッド距離が、コサイン類似度より大幅に良かったです。 マージンを変えたときや、CNNやFCをそれぞれ分けたときにおいても同様の結果が得られました。
また、画像特徴量のノルムの、学習による変化を見てみます。
まず、以下がHingeEucM324のとき。
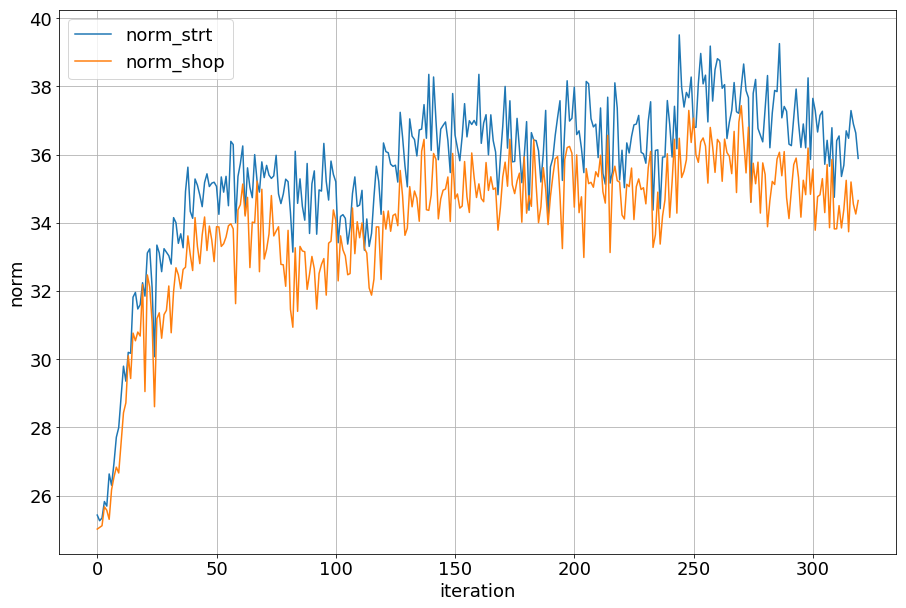
次に、以下がHingeDotM187のとき。
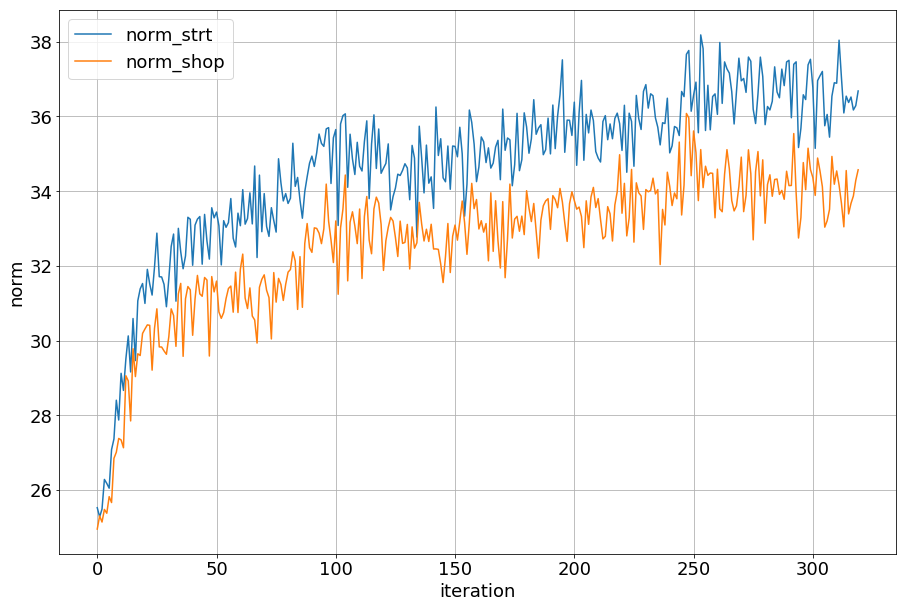
norm_strtがstreet query、norm_shopがshop image、の画像特徴量のノルムを表します。 どちらも 学習につれ特徴量のノルムが大きくなりました。
次に、CNNを分けたときと共有したときの精度の学習による変化を見ます。
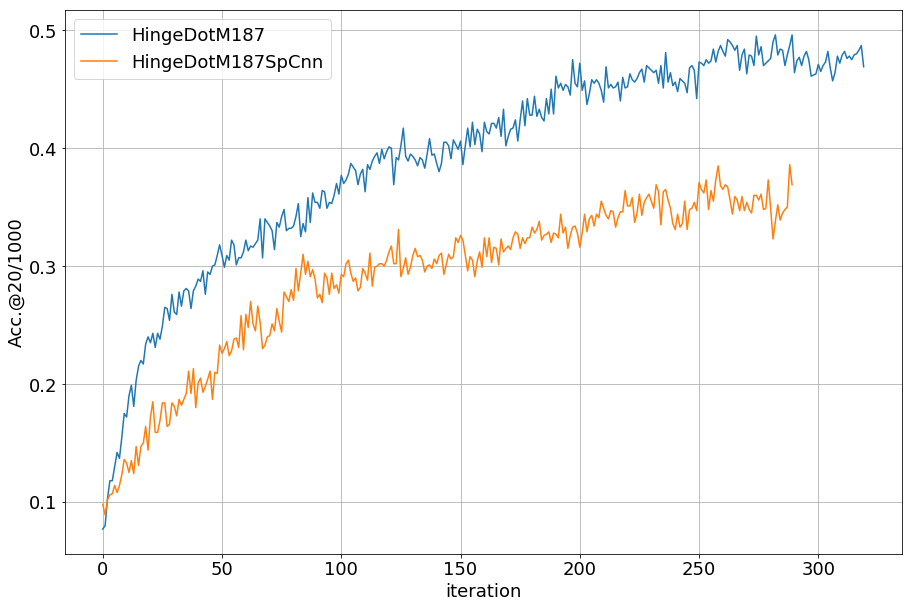
SpCnnと書かれたオレンジの線がCNNを分けた条件で、青い方がCNNを共有した条件です。 CNNを共有したほうが、少ないiterationで良い精度に達しました。
他の計量やマージンを用いたときや、FCを分けときも同様の結果が得られました。
次に、FCを分けたときと共有したときの精度の学習による変化を見ます。
SpFcと書かれたオレンジの線がFCを分けた条件で、青い方がFCを共有した条件です。 FCを分けても、あまり大差はありませんでした。 他の計量やマージンを用いたときや、CNNを分けときも同様の結果が得られました。
次に、損失関数による精度の違いを見てみます。
| 条件 | 計量 | 損失関数 | Acc.@20/1000 |
|---|---|---|---|
| HingeCosM0.5 | コサイン類似度 | hinge loss | 0.283 |
| SceCos | コサイン類似度 | SCE loss | 0.168 |
| 条件 | 計量 | 損失関数 | Acc.@20/1000 |
|---|---|---|---|
| HingeDotM1870 | 内積 | hinge loss | 0.469 |
| SceDot | 内積 | SCE loss | 0.049 |
どちらの計量においても、 損失関数はSCE lossよりhinge lossのほうが良かった です。
考察
CNNの重みを固定すると、FC1層のパラメータによる表現力が足りなかったため、精度が落ちたと考えられます。
コサイン類似度に比べ、内積とユークリッド距離の方が大幅によかった理由は、ノルムを大きくすることでマージンによる悪影響を小さくできたためと考えられます。 ノルムを大きくするとマージンによる影響を小さくできたことについては、付録2で説明します。
fine-grained classificationにおいては、hinge lossよりSCE lossの方が良い結果を出しています。 一方、cross-domain画像検索では、マージンを大きくすることに加え、SCE lossを用いることも有効でないことがわかりました。
まとめ
既存のmetric learningの慣習が必ずしもcross-domain画像検索では有効とは限らないことがわかりました。
また、cross-domain画像検索においてDMLを用いる場合、以下のテクニックが有効だとわかりました。
- 少ないiterationで良い精度に達したければ、CNNは共有にする
- CNNはImageNetの重みからfine-tuningする
- 計量は内積を用いる
- 損失関数はSCE lossでなくhinge lossを用いる
- マージンは大きくしすぎない
付録1：ユークリッド距離のときのマージンの変換の導出
コサイン類似度では、以下のようにpositiveとnegativeの類似度を、最悪でもマージン分だけ差をつけたいです。
$$ \cos{\theta_p} = \cos{\theta_n} + m_{cos} $$
：positiveの角度
：negativeの角度
また、positiveとnegativeの離したい角度をとすると、
と表せます。
このときpositiveとnegativeの距離は、
の成す弦と一致するので、以下で表せます。
$$ m_{euc} = 2 ||x||\sin{\frac{\theta}{2}} $$ $$ =\sqrt{2(1-\cos{\theta})}||x|| $$
今、、
としたいので以下のようになります。
$$ \cos{\theta} $$ $$ =\cos{(\theta_n-\theta_p)} $$ $$ =\cos{\theta_n}\cos{\theta_p} + \sin{\theta_n}\sin{\theta_p} $$ $$ =\sqrt{1-m_{cos}^2} $$
よって、以下の変換を用いました。
$$ m_{euc} := \sqrt{ 2 (1-\sqrt{1-m_{cos}^2}) }||x|| $$
付録2：ノルムを大きくするとマージンの悪影響を減らせる理由
まず、内積のときの場合について説明します。 ノルムが大きくなるにつれ内積も大きくなるので、マージンが相対的に小さくなります。 よって、コサイン類似度に比べ、マージンの影響を受けづらかったのだと考えられます。
また、ユークリッド距離の二乗を展開すると、内積のときと本質的に同じことがわかります。 ユークリッド距離を用いたhinge lossは以下を小さくしたいです。
$$ d_p^2 - d_n^2 $$
：positive pairのユークリッド距離
：negative pairのユークリッド距離
距離を展開します。
$$ d_p^2 - d_n^2 $$ $$ = ||x_a-x_p||^2 - ||x_a-x_n||^2 $$ $$ = - 2x_a^Tx_p + 2x_a^Tx_n + ||x_p||^2 - ||x_n||^2 $$
：anchorの画像特徴量
：positiveの画像特徴量
：negativeの画像特徴量
今、positiveとnegativeのドメインは同じなので、それぞれのノルムは同じとみなすと以下を小さくしたいということになります。
$$ - x_a^Tx_p + x_a^Tx_n $$
つまり、positive pairの内積は大きく、negative pairの内積は小さくしたいということになります。 よって、ユークリッド距離を用いたmetric learningは内積を用いた場合と本質的には同じだと考えられます。 ですから、内積のときと同様の理由で、マージンの影響を受けづらかったのだと考えられます。
最後に
研究所ではcross-domain画像検索以外にも「似合う」ということについて多角的に研究を進めています。機械学習に限らず、専門性を活かしてファッションを分析できる環境を提供しています。ファッションに関する研究テーマに挑戦したい方はぜひ下のリンクから応募して、ぜひ一度オフィスに来ていただければと思います。
